1) Donner les formes canoniques des fonctions suivantes :
a) $f_1(x)=2x^2+8x–1$
b) $f_2(x)=–3x^2–12x–8$
c) $f_3(x)=2x^2+2x+6$
d) $f_4(x)=x^2–3x+3$
2) Trouver la courbe correspondante à chacune des fonctions ci-dessous :
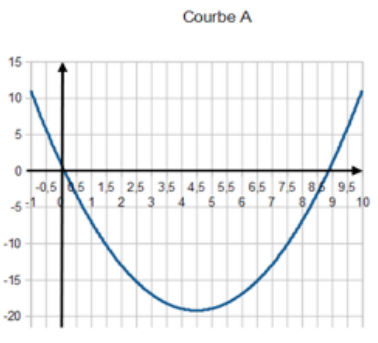
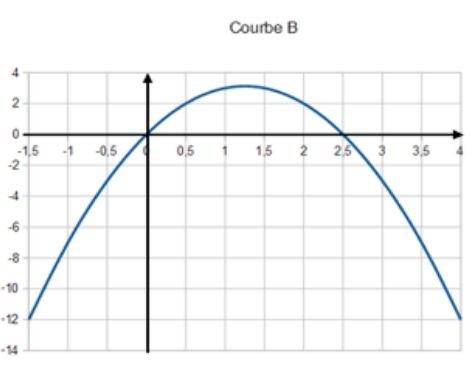
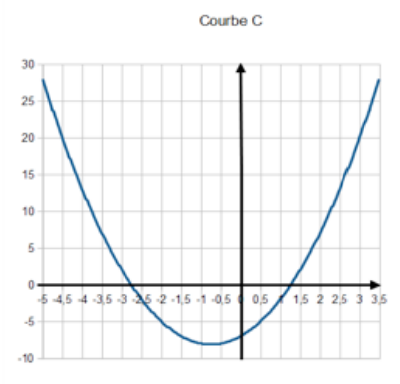
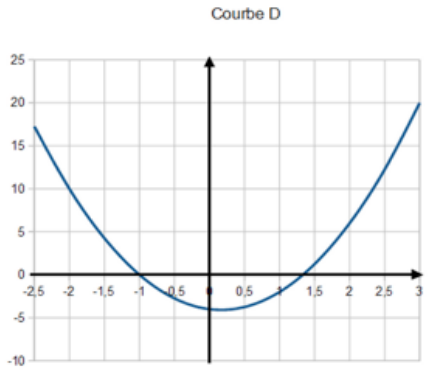
a) $f_1(x)=2x^2+3x–7$
b) $f_2(x)=x^2–9x+1$
c) $f_3(x)=3x^2–x–4$
d) $f_4(x)=–2x^2+5x$
Justifiez vos résultats.
a) $f_1(x) = 2x^2 + 8x – 1$
$f_1(x) = 2 (x^2 + 4x) – 1$
$f_1(x) = 2 [(x + 2)^2 – 4] – 1$
$f_1(x) = 2 (x + 2)^2 – 9$
b) $f_2(x) = – 3x^2 – 12x – 8$
$f_2(x) = – 3 (x^2 + 4x) – 8$
$f_2(x) = – 3 [(x + 2)^2 – 4] – 8$
$f_2(x) = – 3 (x + 2)^2 +4$
c) $f_3(x) = 2x^2 + 2x +6$
$f_3(x) = 2 (x^2 + x) + 6$
$f_3(x) = 2\left[\left(x +\dfrac{1}{2}\right)^2 - \dfrac{1}{4}\right] + 6$
$f_3(x) = 2\left(x + \dfrac{1}{2}\right)^2 + \dfrac{11}{2}$
d) $f_4(x) = x^2 – 3x + 3$
$f_4(x) =\left(x – \dfrac{3}{2}\right)^2 – \dfrac{9}{4} + 3$
$f_4(x) =\left(x – \dfrac{3}{2}\right)^2 +\dfrac{3}{4}$
2) On peut tout simplement calculer $f(0)$ dans chaque cas ou écrire les fonctions sous forme canonique :
a) $f_1$ → courbe C
b) $f_2$ → courbe A
c) $f_3$ → courbe D
d) $f_4$ → courbe B
