L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Soit l'expression \(-4(x+5)^2+8\). Quelles sont les propositions correctes :
Sa forme développée est \( -4x^2-40x-92\).
Sa forme développée est \( -4x^2-92\).
La parabole associée a ses branches tournées vers le haut.
La parabole associée admet pour maximum le point de coordonnées \(S(5 ; 8)\).
Quel est le signe de \(a\) ?
Quelle est l'allure de la parabole ?
Est-on en présence d'un minimum ou d'un maximum ?
Ici on a : \(a = - 4\) donc \(a < 0\) ; les branches de la parabole sont orientées vers bas et on est en présence d'un maximum !
La forme canonique donne directement les coordonnées du sommet mais attention aux signes :
\(-4(x+5)^2+8= -4(x-(-5))^2+8\) donc \(\alpha=-5\) et \(\beta=8\) et \(S(- 5 ; 8) \).
\(\begin{align*}-4(x+5)^2+8= -4(x^2+10x+25)+8 &\Leftrightarrow 4(x+5)^2 +8 = -4x^2-40x-100+8\\ &\Leftrightarrow 4(x+5)^2 +8 =-4x^2-40x-92 \end{align*}\)
Question 2
Une fonction polynôme du second degré dont le tableau de variations est donné ci-dessous peut-être définie par :
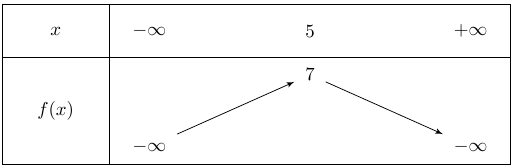
\(f(x) = - x² + 10 x - 13\)
\(f(x) = - x² + 5 x + 7\)
\(f(x) = x² + 7 x - 5\)
\(f(x) = - x² + 10 x - 18\)
Quelle est l'allure de la parabole et donc le signe de \(a \) ?
Quelle est l'image de \(5\) ?
Quelles sont les coordonnées du sommet de la parabole ? Calculer \(\alpha\) !
On sait que \(a < 0\).
On a \(f(5) = 7\).
Or pour la proposition 1 : \(f(5) = - 25 + 50 – 13\) soit \(f(5) = 12\)
Pour la proposition 2 : \(f(5) = - 25 + 25 +7 = 7\)
Pour la proposition 3 : \(f(5) = 25 + 35 -5 = 55\)
Pour la proposition 4 : \(f(5) = - 25 + 50 – 18 = 7\)
On peut écarter les propositions 1 et 3 !
De plus, pour la proposition 2 on a :
\(\alpha = -\dfrac{b}{2a} =-\dfrac{5}{-2} =2.5 \)
impossible car on sait avec le tableau que \(\alpha=5\) .
La proposition 4 est donc juste
Question 3
Quelles sont les variations de la fonction \( f\) définie sur \(\mathbb{R}\) par \( f(x)= -2x+4x^2\) ?
\(f\) est croissante puis décroissante.
\(f\) est décroissante puis croissante.
\(f\) est croissante sur \(\mathbb{R}\).
\(f\) est décroissante sur \(\mathbb{R}\).
Quel est le signe de \(a\) ?
Quelle est alors l'allure de la parabole ?
Pour éviter les erreurs (et les pièges !) attention à bien écrire \(f\) sous la forme donnée dans le cours :
\(f(x)=-2x+4x^2\) donc \(f(x)=4x^2-2x\) et finalement \(a = 4 \) (\(a > 0\))
Question 4
Soit le trinôme \(f(x)= -3(x+3)^2-5\) et \(\mathscr{C}_f\) sa courbe représentative dans un repère du plan.
\(f(x)= -3(x-1)(x+7)\)
\(\mathscr{C}_f\) coupe l'axe (\(Oy\)) au point \(A(0;-32)\).
\(\mathscr{C}_f\) coupe l'axe (\(Ox\)) en 2 points distincts.
L'équation \(f(x)=25\) admet 2 solutions distinctes dans \(\mathbb{R}\).
Déterminer l'intersection de \(\mathscr{C}_f\) et (\(Oy\)), c'est calculer une image. Laquelle (vous pouvez vous aider d’un petit schéma) ?
Déterminer l'intersection de \(\mathscr{C}_f\) et (\(Ox\)), c'est résoudre équation. Laquelle ?
Pour la première, il faut calculer l'image de \( 0\)
Pour la seconde, il faut résoudre $-3(x+3)^2-5=25$
Pour la proposition 1 on peut la développer, mais on peut aussi calculer l'image de \( 0\) :
\(f(0) = -(0-1)(0+7) = 21 \)
Or d'après l'énoncé \( f(0)= -3(0+3)^2-5=-32 \).
La proposition 1 est donc fausse.
Proposition 2 : \(f(0) = - 32\) nous donne la réponse cherchée !
La proposition 2 est juste !
Proposition 3 : on résout l'équation \(f(x) = 0\)
Pour tout \(x\) de \( \mathbb{R}\) :
\(\begin{align*} f(x) = 0 & \Leftrightarrow -3(x+3)^2-5= 0 \\ &\Leftrightarrow -3(x+3)^2=5 \\ &\Leftrightarrow (x+3)^2=-\frac{3}{5} \end{align*} \)
Impossible ! (Un carré ne peut être négatif !) La parabole ne coupe donc jamais l’axe des abscisses.
Pour tout \(x\) de \(\mathbb{R}\) :
\(\begin{align*}f(x) = 25 &\Leftrightarrow -3(x+3)^2-5=25\\ &\Leftrightarrow -3(x
Question 5
La forme canonique du trinôme \(f(x) = -5(x-1)^2 +2(x+1)(x-3)\) est :
\(3(x-1)^2 -8\)
\(3(x-1)^2 +8\)
\(-3(x-1)^2 -8\)
\(-3(x-1)^2 +8\)
Quelle est la forme développée de \(f\) ?
Trouver alors sa forme canonique !
Forme développée de \(f\) :
\( \begin{align*}f(x)=-5(x-1)^2+2(x+1)(x-3) &\Leftrightarrow f(x)=-5(x^2-2x+1)+2(x^2-2x-3)\\ &\Leftrightarrow f(x)=-5x^2+10x-5+2x^2-4x-6\\ &\Leftrightarrow f(x)=-3x^2+6x-11 \end{align*}\)
Forme canonique de \(f\):
\( \begin{align*}f(x)=-3x^2+6x-11 &\Leftrightarrow f(x)=-3(x^2-2x)-11\\ &\Leftrightarrow f(x)=-3((x-1)^2-1)-11\\ &\Leftrightarrow f(x)=-3(x-1)^2+3-11\\ &\Leftrightarrow f(x)=-3(x-1)^2-8 \end{align*}\)
