L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Parmi les expressions proposées reconnaître les trinômes du second degré.
\(7x^2-6x+\sqrt 2 \)
\(-3x^2+2\sqrt x + 5 \)
\(2(x-3)^2+(x-1)(x-5) \)
\(8-x \)
Il faut effectuer les calculs sauf pour la proposition 1 !
Quelle est la forme possible d'un trinôme du second degré ?
Peut-on avoir \(a = 0\) ?
Quant à la 3 elle donne :
\( \begin{align*} 2(x-3)^2 + (x-1)(x+5) &= 2(x^2-6x+9) + x^2 +4x -5 \\
& =2x^2-12x+18+x^2+4x-5 \\ & = 3x^2-8x+13\end{align*} \)
La proposition 2 est fausse à cause de \(\sqrt x\) et la 4 ne comporte pas de terme en \(x^2\).
On peut avoir \(b=0\) et / ou \(c=0\).
Question 2
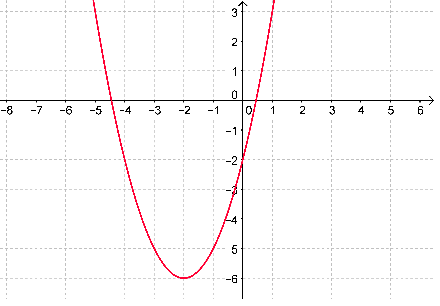
La courbe ci-contre est celle d'une fonction polynôme du second degré.
Avec les notations du cours :$f(x) = a(x-\alpha)^2+\beta$ on a :
\(a = 1 \quad \alpha = -2 \quad \beta = -6\)
\(a = -1 \quad b = 4 \quad c = -2\)
\(a = 1 \quad \alpha = 2 \quad \beta = -6\)
\(a = 1 \quad b=4 \quad c=2\)
Quel est le signe de \(a\) ?
Quelles sont, graphiquement, les coordonnées du sommet ?
Sur le graphique on lit que les coordonnées du sommet sont \((- 2 ; - 6)\). Le cours nous indique qu'elles sont aussi (\(-\frac{b}{2a}; f(-\frac{b}{2a})\)) ou encore( \(\alpha;\beta\)). La proposition 2 est à éliminer car \(a\) doit être positif, tout comme la proposition 4 (car l’image de \(0\) est \(f(0)=-2\) sur le graphique, soit \(c=-2\)).
Question 3
Le trinôme \(f(x)=-2(x+5)^2-\large \frac{1}{2}\) admet :
Pour minimum \(\dfrac{1}{2}\) en \( x = 5\)
Pour minimum \(-\dfrac{1}{2}\) en \( x = -5\)
Pour maximum \(-\dfrac{1}{2}\) en \( x = -5\)
Pour maximum \(-\dfrac{1}{2}\) en \( x =5\)
Quel est le signe de \(a\) ?
Cherche-t-on un maximum ou bien un minimum ?
Sous quelle forme est le trinôme ?
Quelles sont les coordonnées du sommet et donc la valeur de l'extremum cherché ?
Un extremum est un maximum ou un minimum; ici on cherche un maximum car \(a = - 2\) et donc \(a < 0\).
Il ne faut pas confondre le maximum avec la valeur de \(x\) à laquelle il correspond.
Quand on dit que les coordonnées du sommet de la parabole sont (\(\alpha;\beta\)) cela signifie que l'extremum est \(\beta\) et qu'il est atteint lorsque \(x\) vaut \(\alpha\).
Question 4
La forme canonique du trinôme \(f(x)= 2x^2 -12x+23\) est :
\(f(x)= 2(x-3)^2 + 5\)
\(f(x)= 2(x+3)^2 + 5\)
\(f(x)= 2(x-3)^2 + 4\)
\(f(x)= -2(x-3)^2 + 1\)
Que vaut \(a\) ? Quelle proposition peut-on alors écarter ?
Il n'y a pas d'autres choix que de faire les calculs !
Méthodes pour obtenir la forme canonique d'un trinôme:
Méthode 1 : Retenir et appliquer les formules sur \(\alpha\) et \(\beta\) :
\(\alpha=-\dfrac{b}{2a} = -\dfrac{12}{4}=3 \) et donc \(\beta = f(3) = 5\).
Méthode 2 : Sans formule à apprendre, il faut juste suivre les étapes suivantes :
$f(x) = 2x^2-12x+23$
$\iff f(x)=2(x^2-6x)+23$
$\iff f(x)=2((x-3)^2-9)+23$
$\iff f(x)=2(x-3)^2-18+23$
$\iff f(x)=2(x-3)^2+5$
Question 5
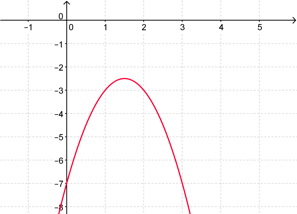
\( y = -2x^2+6x-3\)
\( y = 2x^2+12x-3\)
\( y = -2x^2+3x-7\)
\( y = -2x^2+6x-7\)
Quel est le signe de \(a \) ? Quelle proposition peut-on alors écarter ?
Lire graphiquement l'image de \(0\) puis déterminer cette image pour chaque proposition : cela te permets d’écarter encore quelques propositions.
Aide-toi d’un dernier point : par exemple, utilise le graphique pour trouver l’image de \(1\), puis calcule là avec les formules restantes pour voir laquelle peut convenir.
Lire graphiquement l'abscisse du sommet de la parabole puis déterminer la valeur de cette abscisse pour chaque proposition.
Le signe de \(a\) s’obtient grâce à la forme de la parabole (certes, cela ne suffit pas à connaître la valeur de \(a\), on ne peut pas tout avoir ! Mais c’est assez pour éliminer quelques réponses). L'image de \(0\) permet de trouver la valeur de \(c\) !
Pour trancher entre les propositions 3 et 4, il suffit d’utiliser un point de la courbe : celui d’abscisse \(1\)(ou \(2\)) par exemple.