Dans un repère orthonormé, on donne les points $A(1 ;-2), B(2 ;3)$ et $ C(-2 ;8)$ et le vecteur $\vec{u} \displaystyle \binom{-2}{3}$
Soit de plus $d$ la droite d’équation $-4x+y+2=0$.
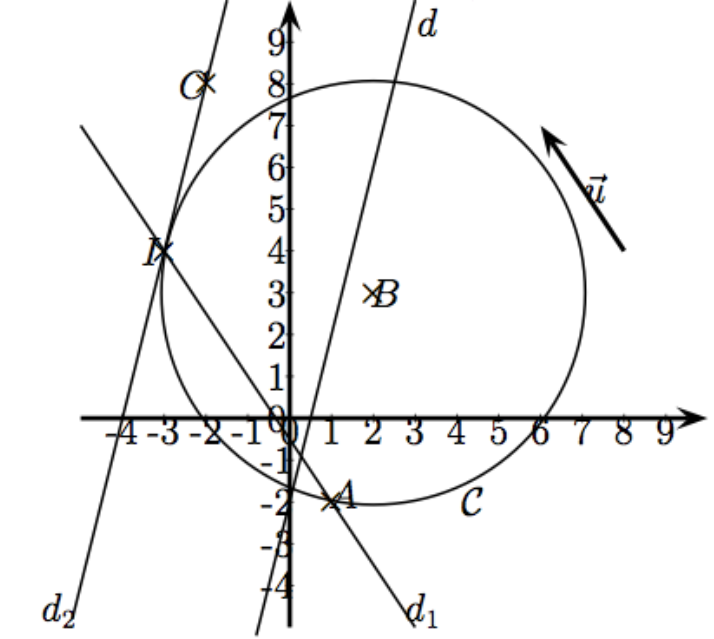
1) Sur une figure placer ces trois points, tracer la droite $d$, et représenter le vecteur $\vec{u}$.
2) Déterminer une équation cartésienne de la droite $d_1$ passant par $A$ et de vecteur directeur $\vec{u}$.
3) Déterminer une équation de la droite $d_2$ parallèle à $d$ et passant par $C$ puis la tracer.
4) Justifier que les droite $d_1$ et $d_2$ sont sécantes, puis déterminer les coordonnées de leur point d’intersection $I$.
5) Calculer $AB$.
6) Quelle est la nature du triangle $ABI$ ?
7) On note $C$ le cercle de centre $B$ et rayon $AB$.
a) Soit $M(x;y)$ un point du cercle $C$. Montrer que les coordonnées du point $M$ vérifient l’équation $(x − 2)^2 + (y − 3)^2 = 26$.
b) Déterminer le nombre de points d’intersection du cercle $C$ et de la droite $d$.
1)
2) $\vec{u}$ est un vecteur directeur de $d_1$ qui a donc une équation de la forme $3x+2y+c=0$ avec $c$ réel.
Or $A \in d_1 \iff 3 \times 1 + 2 \times (-2) +c = 0 \iff c=1$
Une équation de $d_1$ est donc $3x+2y+1=0$.
3) $\vec{v} \displaystyle\binom{1}{-4}$ est un vecteur directeur de $d$ donc aussi de $d_2$ car $d_2 // d_1 $ et $d_2$ a une équation de la forme : $ -4x +y +c = 0 $
Or $ C \in d_2$ donc :
$ -4 \times (-2) +8 +c = 0 \iff c= -16$
Et donc une équation de $d_2$ est : $ -4x +y -16 = 0 $.
4) $\vec{u}$ et $\vec{v}$ sont des vecteurs directeurs de $d_1$ et $d_2$, or $\vec{u}$ et $\vec{v}$ ne sont pas colinéaires car $-2 \times (-4) – 3 \times (-1) = 11 \neq 0$.
Ainsi, $d_1$ et $d_2$ ne sont pas parallèles et sont ainsi sécantes.
Les coordonnées de leur point d’intersection $I(x ;y)$ vérifient alors :
$\begin{cases} 3x+2y+1 =0 \\ -4x+y-16=0 \end{cases}$
$ \iff \begin{cases} 3x+2y+1 =0 \\ -8x+2y-32=0 \end{cases}$
On soustrait la ligne du bas à celle du haut :
$ \iff \begin{cases} 3x+2y+1 =0 \\ 11x+33=0 \end{cases}$
$ \iff \begin{cases} y = 4\\ x = -3 \end{cases}$
Ainsi, le point d’intersection de $d_1$ et $d_2$ est $I(-3 ;4)$.
5) $AB = \sqrt{(2-1)^2 + (3- (-2))^2} = \sqrt{26}$
Ou encore : $AB^2=26$.
6) On a aussi :
$AI^2 =( -3 -1)^2 + (4 – (-2))^2 = 52$, et
$BI^2 =( -3 -2)^2 + (4 – 3)^2 = 26$ .
On a donc $BI = AB$ et aussi $ AB^2 + BI^2 = AI^2$ : le triangle $ABI$ est isocèle et rectangle en $B$ d'après la réciproque de Pythagore.
7) a) $M(x ;y) \in C \iff MB = AB$
$\iff MB^2 = AB^2$
$\iff (x-2)^2 + (y-3)^2 = 26$
Ceci est l’équation cartésienne du cercle $C$.
b) $M(x ;y) \in C \cap d \iff \begin{cases} 4x+y+2 =0 \\ (x-2)^2+(y-3)^2 = 26 \end{cases}$
$ \iff \begin{cases} y= 4x-2 \\ (x-2)^2+(y-3)^2 = 26 \end{cases}$
$ \iff \begin{cases} y= 4x-2 \\ 17x^2 -44x + 3 = 0 \end{cases}$
La deuxième équation, du $2 ^{nd}$ degré, a pour discriminant
$\Delta = (-44)^2 – 4 \times 3 \times 17 = 1732 > 0$ ,
Elle admet donc deux solutions réelles distinctes. $C$ et $d$ ont deux points d’intersection distincts.
