Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Équation cartésienne de cercle
Pour trouver l'équation d'un cercle, il existe deux manières de procéder selon que l'on dispose du centre et du rayon ou du diamètre.
1) Avec le centre $\Omega (a; b)$ et le rayon $r$
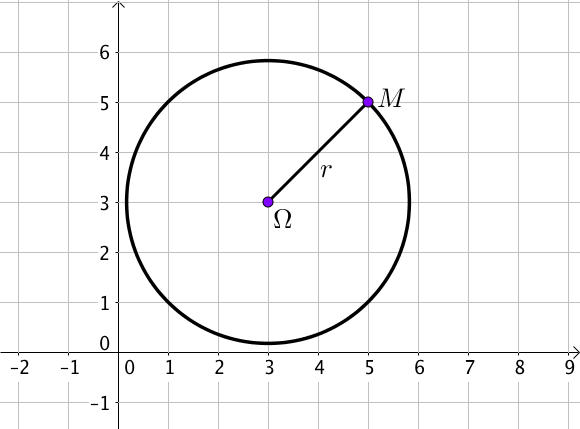
Soit $M(x; y)$ un point du cercle,
Alors ${\Omega M}^2 = r^2$.
Ainsi, $(x - a)^2 + (y - b)^2 = r^2$.
Exemple :
Si $\Omega (-1; 2)$ et $r = 3$, alors l'équation réduite du cercle est
$(x - (-1))^2 + (y - 2)^2 = 3^2$ c'est à dire :
$(x + 1)^2 + (y - 2)^2 = 9$.
2) Avec le diamètre $[AB]$
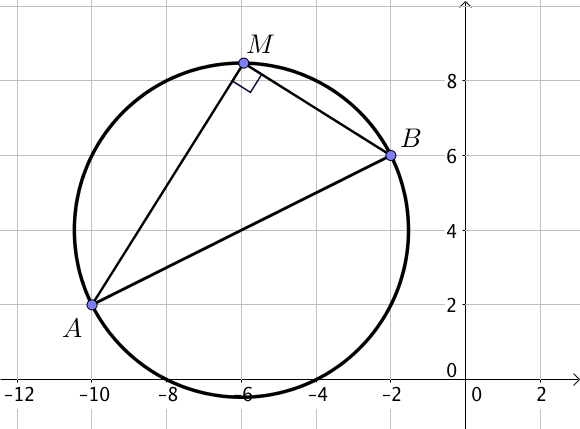
Soit $M$ un point du cercle,
alors le triangle $ABM$ est rectangle en $M$ car $[AB]$ est un diamètre du cercle et l'hypoténuse du triangle.
Ainsi, les droites $(MA)$ et $(MB)$ sont
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
