Fiche de cours
Vecteur normal à une droite
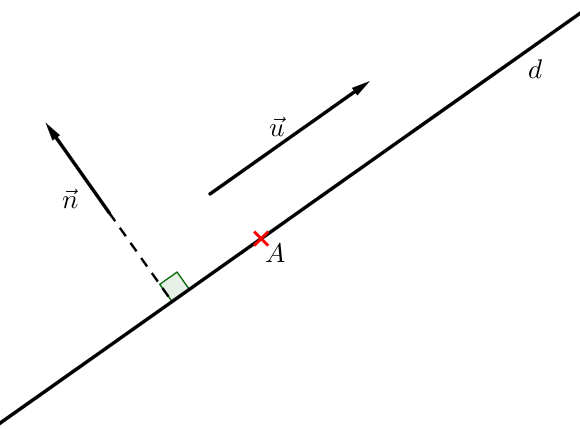
Une droite peut être définie à partir d'un de ses vecteurs directeurs. ($\overrightarrow{u}$ sur la figure)
Elle peut également l'être à partir de l'un de ses vecteurs normaux. ($\overrightarrow{n}$ sur la figure)
Définition :
Un vecteur normal est un vecteur orthogonal à tout vecteur directeur de la droite.
Tout vecteur colinéaire à un vecteur normal est normal à la droite.
Soient $M$ un point quelconque de la droite $(d)$, $A$ un point appartenant à la droite.
Si $\overrightarrow{n}$ est un vecteur normal à cette droite, alors :
$\overrightarrow{AM}.\overrightarrow{n} = 0$.
Vecteur normal et équation cartésienne de droite
On se place dans un repère.
On peut donc écrire les coordonnées des différents éléments précédents :
$\overrightarrow{n} \left ( \begin{array}{c} a \\ b \\ \end{array} \right )$, $M(x; y)$ et $A(x_A; y_A)$.
L'équat
