L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Quelles sont la ou les propositions correctes ? Soient \(\overrightarrow{u}\begin{pmatrix} 2 \\ -4 \end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} \sqrt2\\ -\sqrt8 \end{pmatrix}\). Alors :
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont orthogonaux.
\(\overrightarrow{u}= k\overrightarrow{v}\) avec \(k\) réel strictement positif.
\(\overrightarrow{u}= k\overrightarrow{v}\) avec \(k\) réel strictement négatif.
\(\overrightarrow{u}.\overrightarrow{v}= 10\sqrt2\)
Quel renseignement as-tu sur les vecteurs ? Leurs normes ? L'angle qu'ils forment ? Leurs coordonnées ?
Calcule alors \(\overrightarrow{u}.\overrightarrow{v}\)
\(\overrightarrow{u}= k\overrightarrow{v}\) signifie que \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires; pour le savoir on peut utiliser les coordonnées de chaque vecteur ou bien appliquer le critère de colinéarité vu en 2de.
On rappelle que \(\overrightarrow{u}\) et \(\overrightarrow{v}\)sont orthogonaux si et seulement si \(\overrightarrow{u}.\overrightarrow{v}= 0\) .
Appliquer le critère de colinéarité permet juste de déterminer si les vecteurs sont ou non colinéaires. Cela ne permet pas de déterminer la valeur du réel \(k\) tel que \(\overrightarrow{u}=k\overrightarrow{v}\) Ici le critère de colinéarité donne :\(2\times(-\sqrt8) + (4)\times(-\sqrt2) = 0\) donc \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires .
En fait on a \(\overrightarrow{u}\begin{pmatrix} 2 \\ -4 \end{pmatrix}\) et \(\overrightarrow{v}\begin{pmatrix} \sqrt2\\ -\sqrt8 \end{pmatrix}\).soit \(\overrightarrow{v}\begin{pmatrix} \sqrt2\\ -2\sqrt2 \end{pmatrix}\). Il est donc évident, à la lecture des coordonnées que \(\overrightarrow{u}=\sqrt2 \overrightarrow{v}\)
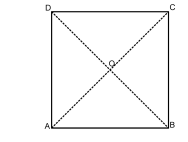
Question 2
\( \overrightarrow{DB}.\overrightarrow{DC} = a^2\)
\( \overrightarrow{OD}.\overrightarrow{DC} = \dfrac{1}{2}a^2\)
\( \overrightarrow{OD}.\overrightarrow{OC} = a\)
\( \overrightarrow{AO}.\overrightarrow{AC} = a^2\)
Ici on doit effectuer les calculs en fonction de \(a\).
Calcule chaque produit scalaire en utilisant le projeté orthogonal.
\(O\), le centre du carré, est le milieu de chaque diagonale. Son projeté orthogonal sur \([AB]\) est le milieu \(I\) de \([AB]\) et en particulier : \(AI = \frac{1}{2} AB\)
Les diagonales d'un carré sont perpendiculaires…
\(C\) est le projeté orthogonal du point \(B\) sur la droite \((DC)\) et donc :
\(\overrightarrow{DB}.\overrightarrow{DC}= \overrightarrow{DC}.\overrightarrow{DC} \) soit :
\( \overrightarrow{DB}.\overrightarrow{DC} =a^2\)
\(\overrightarrow{AB}= -\overrightarrow{CD}\) et donc :
\( \overrightarrow{AB}.\overrightarrow{CD}= -\overrightarrow{CD}.\overrightarrow{CD}=-CD^2 = -a^2 \)
Pour le calcul de \(\overrightarrow{OD}.\overrightarrow{DC}\) on peut utiliser le projeté orthogonal de \(O\) sur \((DC) \) mais on peut aussi écrire :
\(\overrightarrow{OD}.\overrightarrow{DC} = \frac{1}{2}\overrightarrow{BD} .\overrightarrow{DC} = - \frac{1}{2}\overrightarrow{DB} .\overrightarrow{DC}\)
Finalement, \(\overrightarrow{OD}.\overrightarrow{DC} = \frac{1}{2} a^2\)
Les vecteurs \(\overrightarrow{OD}\) et \(\overrightarrow{OC}\) sont orthogonaux donc \(\overrightarrow{OD}.\overrightarrow{OC}=0\)
\(\overrightarrow{AO}.\over
Question 3
Dans le plan muni d'un repère orthonormé on considère les points \(A(-2;3)\) \(B(-2;-3)\) et \(C(1;1)\).
Alors :
\(\overrightarrow{BA}.\overrightarrow{BC} = 24\)
\(\overrightarrow{BA}.\overrightarrow{BC} = 13\)
\(\cos( \widehat{ABC}) \approx37° \)
\(\cos( \widehat{ABC}) \approx19°\)
Faire une figure.
Avec les coordonnées des points on peut trouver celles des vecteurs \(\overrightarrow{BA}\) et \(\overrightarrow{BC}\).
On peut aussi trouver \(||\overrightarrow{BA}||\) et \(||\overrightarrow{BC}||\).
Calculer ainsi \(\overrightarrow{BA}.\overrightarrow{BC}\).
Utiliser alors une autre expression du produit scalaire pour déterminer le cosinus de l'angle \(\widehat{ABC}\) en résolvant une équation. On en déduira alors une valeur approchée de l'angle \(\widehat{ABC}\)
\(\overrightarrow{BA}\begin{pmatrix} 0\\ 6 \end{pmatrix}\) et \(\overrightarrow{BC}\begin{pmatrix} 3 \\ 4 \end{pmatrix}\) donc \(\overrightarrow{BA}.\overrightarrow{BC} =24\)
D'une part \(\overrightarrow{BA}.\overrightarrow{BC} =||\overrightarrow{BA}|.|\overrightarrow{BC}|| \times \cos( \widehat{ABC})\) avec :
\(||\overrightarrow{BA}|| = \sqrt{(-4)^2+(-3)^2} \) soit
\(||\overrightarrow{BA}|| = 6\) et \(||\overrightarrow{BC}| |= 5\)
Ainsi, \(\overrightarrow{BA}.\overrightarrow{BC} =30 \times \cos( \widehat{ABC})\)
D'autre part \(\overrightarrow{BA}.\overrightarrow{BC} =24\)
Par conséquent : \(30 \times \cos( \widehat{ABC})=24 \Leftrightarrow \cos( \widehat{ABC}) = \frac{24}{30}\)
A l'aide de la calculatrice on obtient : \(\widehat{ABC}\approx 37°\) (attention à l’unité de l’angle : radian ou degré. Ici, il faut mettre le réglage en degré).
Question 4
Dans le plan muni d'un repère orthonormé on considère les points \(A(-2;1)\) \(B(1;2)\) et \(C(4;-1)\). Soit \(H\) le projeté orthogonal du point \(B\) sur la droite \((AC)\).
Alors :
\(\overrightarrow{CA}.\overrightarrow{CB} > 0\)
L'angle \(ACB\) est aigu.
\(\overrightarrow{AC}.\overrightarrow{AB} = 16\)
\(AH = 4\sqrt10\).
Fais une figure !
Utilise les coordonnées pour déterminer les produits scalaires et la longueur \(AH\).
\(\overrightarrow{CA}.\overrightarrow{CB} =||\overrightarrow{CA}||.||\overrightarrow{CB}|| \times \cos( \widehat{ACB})\) Comme \(||\overrightarrow{CA}||\) et \(||\overrightarrow{CB}||\) sont des nombres positifs, le signe du produit scalaire dépend de celui du cosinus de l'angle.
Si l'angle est aigu alors son cosinus est positif et le produit scalaire aussi.
Si l'angle est obtus alors son cosinus est négatif et le produit scalaire aussi !
Dans quelle formule intervient la longueur \(AH\) ?
Pour la proposition 1 : on obteint \(\overrightarrow{CA}.\overrightarrow{CB} = 24\)
La proposition 2 est vraie car le produit scalaire \(\overrightarrow{CA}.\overrightarrow{CB} \)étant positifs alors l'angle \(\widehat{ACB}\) est aigu.
Pour la proposition 3 on obtient : \(\overrightarrow{AC}.\overrightarrow{AB} = 16\)
Pour la proposition 4 :
D'une part \(\overrightarrow{AC}.\overrightarrow{AB} = 10\)
D'autre part \(\overrightarrow{AC}.\overrightarrow{AB} =\overrightarrow{AC}.\overrightarrow{AH}\) soit :
\(\overrightarrow{AC}.\overrightarrow{AB} =AC\times AH\)
Ainsi : \(AC\times AH = 16 \)
\(\Leftrightarrow \sqrt{40}\times AH = 16 \)
\(\Leftrightarrow AH = \large\frac{16}{\sqrt{40}} \)
En multipliant le numérateur et le dénominateur par \(\sqrt{40} \), on obtient \(AH = 4\frac{\sqrt{10}}{5}\).
Question 5
Dans le plan muni d'un repère orthonormé on considère les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) tels que \(||\overrightarrow{u}||=5\) ; \(||\overrightarrow{v}||=4\) et \(\widehat{(\overrightarrow{u};\overrightarrow{v})}= -\dfrac{4\pi}{3} [2\pi]\).
On a :
\(\overrightarrow{u}.\overrightarrow{v}= -10\)
\(\overrightarrow{u}.\overrightarrow{v}= -10\sqrt3\)
\(||\overrightarrow{u}-\overrightarrow{v}||^2 =1 \)
\(||\overrightarrow{u}-\overrightarrow{v}||^2 =61\)
Une seule formule du produit scalaire peut ici être utilisée pour calculer \(\overrightarrow{u}.\overrightarrow{v}\)
\(\cos(-\frac{4\pi}{3}) =-\frac{1}{2}\)
Utilise une nouvelle formule du produit scalaire faisant intervenir \(||\overrightarrow{u}+\overrightarrow{v}||\) pour trouver sa valeur en résolvant une équation.
Attention\(||\overrightarrow{u}-\overrightarrow{v}|| \neq ||\overrightarrow{u}||-||\overrightarrow{v}||\)
\(\overrightarrow{u}.\overrightarrow{v}= ||\overrightarrow{u}||.||\overrightarrow{v}||.\cos(\overrightarrow{u};\overrightarrow{v})\)
donc \(\overrightarrow{u}.\overrightarrow{v}=-10\)
De plus \(\overrightarrow{u}.\overrightarrow{v}= \frac{1}{2}(-||\overrightarrow{u}-\overrightarrow{v}||^2+ ||\overrightarrow{u} ||^2 +||\overrightarrow{v}||^2\)) donc :
\(2 \overrightarrow{u}.\overrightarrow{v} = -||\overrightarrow{u}-\overrightarrow{v}||^2 +||\overrightarrow{u} ||^2 +||\overrightarrow{v}||^2\)
soit : \(||\overrightarrow{u}-\overrightarrow{v}||^2 =- 2 \overrightarrow{u}.\overrightarrow{v}+ ||\overrightarrow{u} ||^2 +||\overrightarrow{v}||^2\)
On a finalement :
\(||\overrightarrow{u}-\overrightarrow{v}||^2 = 25+16-2\times(-10)=61\)