L'énoncé
On considère la fonction \(g(x) = \dfrac{x^2 + x+ 2}{x+2}\) définie et dérivable sur \(D_g=\mathbb{R} \setminus \{-2\}\).
On note \(C_g \) sa courbe représentative.
Question 1
Calculer la dérivée de \(g\) sur son ensemble de définition.
\(g = \dfrac{u}{v}\) avec :
\(u(x) = x^2 + x + 2\) et \(v(x) = x + 2\)
\(u'(x) = 2x + 1 \) et \(v'(x) = 1\)
\(g \) est dérivable sur \( D_g\) et \(g' = \dfrac{u'v -uv'}{v^2}\)
Donc, pour tout \(x \) de \(D_g\) :
\(g '(x) =\dfrac{(2x+1)(x+2) -(x^2 +x+2)}{(x+2)^2} \)
\(g '(x) = \dfrac{2x^2 + 4x + x + 2 -x^2 -x -2}{(x+2)^2}\)
\(g '(x) =\dfrac{x^2 + 4x}{(x+2)^2} \)
\(g '(x) = \dfrac{x(x + 4)}{(x+2)^2}\)
Quelle formule dois-tu utiliser ?
Question 2
Étudier les variations de \(g\) sur \( D_g\).
On a donc :
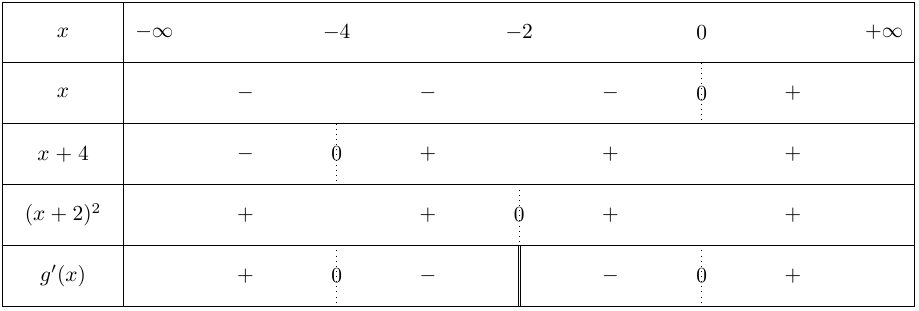
\(g\) est donc croissante sur \(]\infty;-4]\) et sur \([0 ;+\infty[\) et décroissante sur \([-4;-2[\) et sur\( ]-2;0]\)
Quel est le signe de \(g'(x)\) sur \(D_g\)?
Quelles sont alors les variations de \(g\) sur \(D_g\)?
Question 3
Dresser le tableau de variation de \(g\) sur son ensemble de définition.
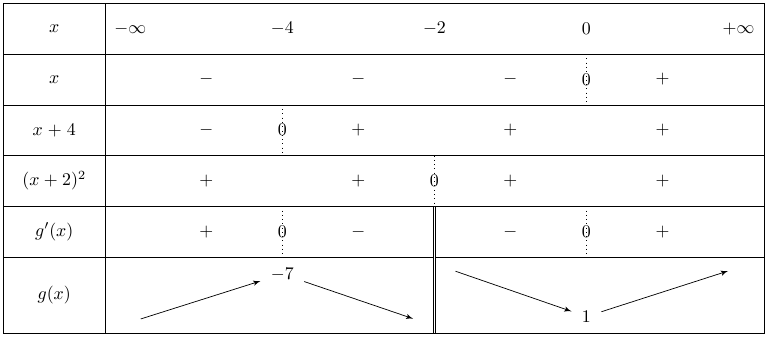
\(g(-4) = \dfrac{16 -4 + 2}{-4+2}\) et \(g(0) = \dfrac{2}{2}\)
\(g(-4) = \dfrac{14}{-2} \) et \(g(0) = 1\)
\(g(-4) = - 7\)
Ton tableau est-il complet ?
Question 4
Donne un encadrement de \(g(x)\) pour \(x\) compris entre \(-1\) et \(0\).
Soit \(x\) un réel de \([ - 1 ; 0]\) . On a donc : \( - 1 \leq x \leq0\)
\(g\) étant décroissante sur \(]-2; 0]\), elle l'est donc aussi sur \([ - 1 ; 0]\) et :
\(g(- 1) \geq g(x) \geq g(0)\)
Soit \(g(0) \leq g(x) \leq g(- 1)\)
Or, \(g(-1) = \large\frac{1 - 1+ 2}{-1+2}\)
Soit : \(g(-1) = 2\)
On sait aussi que \( g(0) =1 \)
Conclusion : Pour tout \(x \in [ - 1 ; 0]\) : \( 1 \leq g(x) \leq 2\)
Quelles sont les variations de \(g\) sur \([ - 1 ; 0]\) ?
Que vallent \(g(-1)\) et \(g(0)\) ?
Question 5
Prouver que l'équation de la tangente \(T\) à \(C_g\) au point d'abscisse \(-3\) est :
\(T\) : \(y = -3x -17\)
\(T\) a pour équation : \( y = g'(-3)(x + 3) + g(3)\)
Or, \(g(-3) = \dfrac{9 - 3 + 2}{ -3 + 2} = - 8\) et
\(g'( -3) = \dfrac{(-3(-3+4)}{(-3+2)^2}= - 3\)
Donc, \(T : y = -3(x + 3) - 8\)
Soit finalement : \(T : y = - 3x - 17\)
Que vaut \(g '( -3)\) ? Et \(g(3)\) ?
Question 6
Étudier les positions relatives de \( C_g\) et \(T\) sur l'ensemble \(D_g\).
Pour tout \(x\) de \(D_g\) :
\(g(x) (-3x -17) = \dfrac{x^2 + x+ 2}{x+2}-(-3x -17)\)
\(\Leftrightarrow g(x) -(-3x -17) = \dfrac{x^2 + x+ 2 + (3x +17)(x + 2)}{x+2}\)
\(\Leftrightarrow g(x) -(-3x -17) = \dfrac{4x^2 + 24x+ 36}{x+2}\)
\(\Leftrightarrow g(x) - (-3x -17) = \dfrac{4(x^2 + 6x+ 9)}{x+2}\)
\(\Leftrightarrow g(x) - (-3x -17) = \dfrac{4(x + 3)^2}{x+2}\)
Étudions le signe de \(g(x) -(-3x -17)\) sur \(D_g\) :
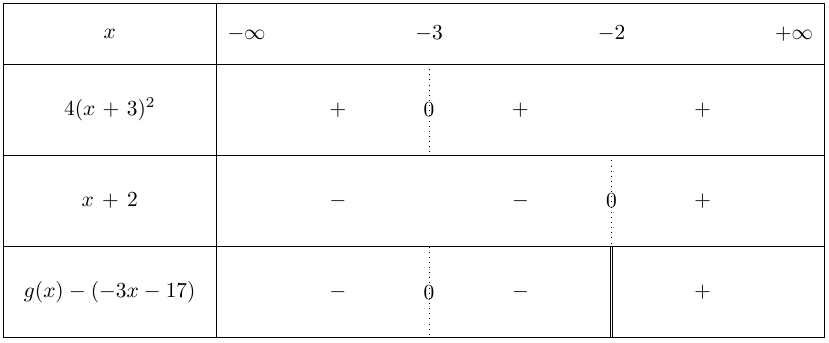
Sur \(]-\infty;-3[ \) et sur \(] -3;-2[\) , \( g(x) -(-3x -17) < 0\) et donc \(C_g\) est au-dessous de \(T\).
Sur\( ]-2;+\infty[, g(x) - (-3x -17) > 0\) et donc \(C_g\) est au-dessus de \(T\).
En \(x = -3, g(x) - (-3x -17) = 0\) et \(C_g\) et \(T\) sont sécantes.

Calculer \(g(x) – (-3x -17)\).
Étudier le signe de \(g(x) – (-3x -17)\).
Conclure !
