L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses
Tu as obtenu le score de
Question 1
On considère le tableau de variation d'une fonction \(f\) définie et dérivable sur \([ - 3;4]\) :
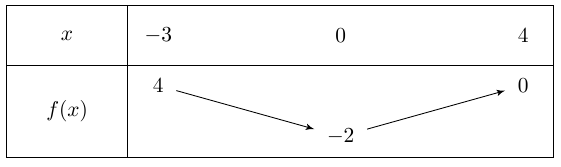
\(f '(x) > 0\) sur \(] - 3 ; 0[\)
\(f '(x) > 0\) sur \(] 0 ; 4[\)
\(f '(x) < 0\) sur \(] 0 ; 4[\)
\(f '(x) < 0\) sur \(] -3;0[\)
Quel est le lien entre variation de \(f\) et signe de \(f '(x)\) ?
Sur \(]- 3;0[ \) comment varie \(f\) ?
Quel est donc le signe de \(f '(x)\) ?
Sur \(]- 3 ; 0[ \ \ f\) est strictement décroissante donc \(f '(x) < 0\).
Sur \(]0 ; 4[ \ \ f\) est strictement croissante donc \(f '(x) > 0\).
Sur \([- 3 ; 0] \ \ f\) est strictement décroissante mais \(f '(x) \leq 0\).
Question 2
On considère une fonction \(f\) dérivable sur \(\mathbb{R}\).
La dérivée de la fonction \(f\) admet la courbe représentative ci-dessous.
\(f\) est décroissante sur \(] –\infty; -1]\).
\(f\) est décroissante sur \(] 3 ; +\infty[\).
\(f\) est croissante sur \(] 1;3[\).
\(f\) est croissante sur \(] 1 ; +\infty[\).
Attention, la courbe donnée est celle de la dérivée \(f '\).
Quel est le lien entre variation de \(f\) et signe de \(f '(x)\) ?
Sur \(] –\infty; -1[ \) quel est le signe de \(f '(x)\) ? Donc comment varie \(f\) ?
Sur \(] –\infty; -1[\) : \(f '(x) < 0\) donc \(f\) est décroissante.
Sur \(] 3 ; +\infty[\) : \(f '(x) < 0\) donc \(f\) est décroissante.
Sur \(]-1 ; 3[\) : \(f '(x) < 0\) donc \(f\) est décroissante.
Sur \(]1 ; +\infty[\), \( f '(x)\) n'a pas un signe constant donc on ne peut rien dire des variations de \(f\).
Question 3
On considère une fonction \(f\) dérivable sur \(\mathbb{R}\) dont la courbe représentative est tracée ci-dessous.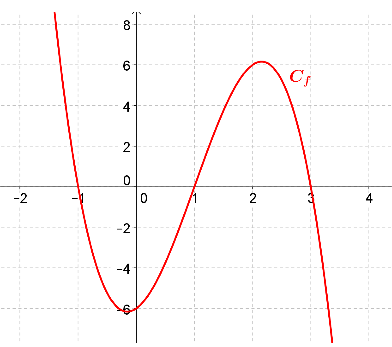
\(f '(x) > 0\) sur \([-2; -2]\)
\(f '(x) > 0\) sur \([-1 ; 2]\)
\(f '(x) > 0\) sur \([0 ; 1]\)
\(f '(x) > 0\) sur \([1 ; 3]\)
Quel est le lien entre variation de \(f\) et signe de \(f '(x)\) ?
Sur \([-2; -2] \) comment varie \(f\) ?
Quel est donc le signe de \(f '(x)\) ?
Et sur \([-1 ; 2] \) ?
\([0 ; 1] \) ?
\([1 ; 3] \) ?
Sur les intervalles \([-2; -2], [-1 ; 2]\) et \([1 ; 3] \ f\) ne garde pas des variations constantes ; on ne peut donc rien dire sur le signe de \(f '(x)\) sur ces intervalles.
Sur \([0 ; 1]\), \(f\) est croissante donc \(f '(x) > 0\).
Question 4
On considère une fonction \(f\) dérivable sur \(\mathbb{R}\) dont la courbe représentative est tracée ci-dessous.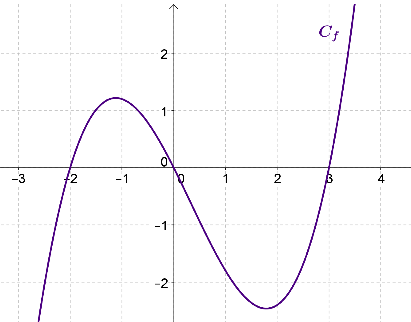
\(f '(x) < 0\) sur \( [0 ; 3]\)
\(f '(x) < 0\) sur \( ]-1; 1,5[\)
\(f '(x) < 0\) sur \( ]-\infty ;-2[\)
\(f '(x) < 0\) sur \( [2 ; +\infty[\)
Quel est le lien entre variation de \(f\) et signe de \(f '(x)\) ?
Sur \([0 ; 3] \) comment varie \(f\) ?
Quel est donc le signe de \(f '(x)\) ?
Et sur \(]-1; 2[ \) ?
\(]-\infty ;-2[ \) ?
\( [2 ; +\infty[ \) ?
Sur \(]-1; 1,5[ : f \) est décroissante donc \(f '(x) < 0\).
Sur \(]-\infty ;-2[ : f \) est croissante donc \(f '(x) >0\).
Sur \([2;+\infty[ : f\) est croissante donc \(f '(x) > 0\).
Sur \([0 ; 3] : f\) n'a pas des variations constantes donc \(f '(x)\) n'a pas non plus un signe constant.

