L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = -2x^2 +4x + 1. \ f \) est dérivable sur \(\mathbb{R}\) et :
\(f '(x) = -4x+4\).
\(f '(x) = -2x - 4\)
$f'(x)= -2x+4$
$f'(x)=2x+4$
\( f\) est un polynôme donc sa dérivée est … ?
Quel est le signe d'une fonction affine sur \(\mathbb{R}\) ?
\(f\) est dérivable sur \(\mathbb{R}\) et pour tout \(x\) de \(\mathbb{R} ,\ f '(x) = -2 \times2x +4\) soit \(f '(x) = -4x+4\).
\( f '(x)\) est une fonction affine qui s'annule pour \(x = 1\).
Question 2
Soit la fonction \(f\) définie sur \(\mathbb{R} \setminus \{-4\} \) par \(f(x) = \dfrac{-x+3}{x + 4}\) et dérivable sur \(\mathbb{R} \setminus \{-4\}.\)
\(f '(x) = -\dfrac{7}{(x+4)^2}\)
\(f '(x) = \dfrac{7}{(x+4)^2}\)
\(f\) est croissante sur \( ] –\infty ; -4[ \) et sur \(] -4 ; +\infty[\)
\(f\) est décroissante sur \( ] –\infty ; -4[ \) et sur \(] -4 ; +\infty[\)
\(f\) est-elle un quotient ? Un produit ?
Quelle formule doit-on alors utiliser pour le calcul de \(f '(x)\) ?
Quel est le signe de cette dérivée ?
\(f =\dfrac{u}{v}\) avec :
\(u(x) = -x+3\) et \(v(x) = x + 4\)
\(u '(x) = -1 \) et \(v '(x) = 1\)
\(f\) est dérivable sur \(\mathbb{R} \setminus \{4\}\) et \(f ' = \dfrac{u'v – uv'}{v^2}\) donc :
Pour tout \(x\) de \(\mathbb{R} \setminus \{4\}\), \(f '(x) = \dfrac{-x-4 + x - 3}{(x + 4)^2}\)
\(f '(x) = -\dfrac{7}{(x + 4)^2}\)
Pour tout \(x\) de \(\mathbb{R} \setminus \{4\} : -7 < 0\) et \( (x+4)^2 > 0\) donc \(f '(x) < 0\) et \( f\) est décroissante sur \( ]–\infty;-4[\) et sur \( ]-4;+\infty[\).
Question 3
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par : \(f(x) =-2 x^3 + 3x^2 + 36x - 1\).
\(f '\) admet deux racines.
\(f\) est décroissante sur \(]–\infty; -2]\)
\(f '(x) < 0\) sur \([ - 2;3]\)
\(f\) est croissante sur \([–2;3]\)
Les racines de \(f '\) sont les valeurs pour lesquelles \(f '(x) = 0\).
Quelle est l'expression de \(f '(x)\) ? Son signe ?
\(f\) est dérivable sur \(\mathbb{R}\) et pour tout \(x\) de \(\mathbb{R}\) : \( f '(x) = -6x^2 + 6x+36\)
Pour tout \(x\) de \(\mathbb{R}\) : \(f '(x) = 0 \Leftrightarrow -6x^2 + 6x+36= 0\)
Le discriminant de ce polynôme vaut \(\Delta = 900\)
\(\Delta > 0\) donc l'équation \(f '(x) = 0\) admet deux solutions : \(x_1 = - 2\) et \(x_2 = 3\)
De plus :
Sur \(]-\infty; -2]\) et \([3; +\infty[\), \(f '(x) \leq 0\) (car du signe de \(a = -6\)) et \(f\) est décroissante.
Sur \([-2;3], f '(x)\geq 0 \) et \(f\) est croissante.
Question 4
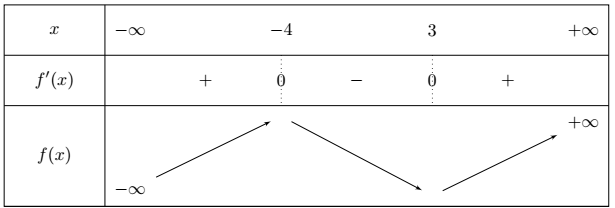
Soit \(f\) une fonction dérivable sur \(\mathbb{R}\) et telle que \(f ' (x) = x^2 + x - 12\)
\(f\) est décroissante sur \([-4 ; 3]\).
\(f\) admet un minimum en \(-4\).
\(f\) admet un minimum local en \(3\).
\(f\) est croissante sur \([- 4;3]\).
Attention : on donne l'expression de \(f '(x)\) !
Quel est son signe ?
Dresse le tableau de variation de \(f\) pour déterminer son maximum et son minimum sur \(\mathbb{R}\) (s'il(s) existe(nt)) puis sur des intervalles restreints.
Pour tout réel \(x\) , \(f ' (x) = x^2 + x - 12\)
Le discriminant de ce polynôme vaut : \(\Delta = 49\)
\(\Delta > 0\) donc \(f '(x)\) admet deux racines :
\(x_1 = - 4\) et \(x_2 = 3\)
La proposition 1 est donc vraie.
En \(x =3\), \(f\) n'admet pas de minimum absolu mais admet un minimum local.
Cela signifie que sur l'intervalle \([-4;+\infty[ \), \(f\) admet un minimum en \(3\) mais pas sur \(\mathbb{R}\).
Question 5
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par : \(f(x) = -x^4 + 6x^2 +8x + 1\)
\(f '(x) = 4(2 - x)(x + 1)^2\)
\(f '(x) =-4x^3 + 12x + 8\)
\(f\) est décroissante sur \([-1;+\infty[\)
\(f\) est croissante sur \(]-\infty;2]\)
Calcule \(f '(x)\).
Tu peux développer les expressions proposées pour déterminer celles qui sont égales à \(f '(x)\).
Quel est le signe de \(f '(x)\) ?
\(f\) est dérivable sur \(\mathbb{R}\), et pour tout \(x\) de \(\mathbb{R}\), on a :
\(f '(x) = -4x^3 + 12x + 8 \)
Pour tout \(x\) de \(\mathbb{R}\),
\(4(2 - x)(x + 1)^2 = (8 – 4x)(x^2 + 2x + 1)\)
\(\Leftrightarrow 4(2 - x)(x + 1)^2 = 8x^2 + 16x + 8 - 4x^3 - 8x^2 - 4x\)
\(\Leftrightarrow4(2 - x)(x + 1)^2 = -4x^3 + 12x + 8\)
\(\Leftrightarrow4(2 - x)(x + 1)^2 = f '(x) \)
Signe de \(f '(x) = 4(2 - x)(x + 1)^2\)
Pour tout \(x\) de \(\mathbb{R}\), \(4(x + 1)^2 \geq 0 \) donc \(f '(x) \) est du signe de \((2 - x)\)
Sur \( ]-\infty;2[, (2 - x) > 0\) donc \( f '(x) > 0 \) et \(f\) est croissante.
Sur \( ]2; +\infty[, (2 - x) < 0 \) donc \(f '(x) < 0 \) et \( f\) est décroissante.
