Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Variations de fonctions
Propriété :
Soit $f$ une fonction dérivable sur $I$,
si pour tout $x \in I$, la dérivée est strictement positive alors la fonction $f$ est strictement croissante sur $I$.
si pour tout $x \in I$, la dérivée est strictement négative alors la fonction $f$ est strictement décroissante sur $I$.
Pour étudier les variations d'une fonction, on commence par calculer la dérivée de la fonction puis on étudie le signe de la dérivée.
On conclut enfin sur les variations de la fonction.
Exemple :
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x^2 + 3x + 1$ et dérivable sur $\mathbb{R}$.
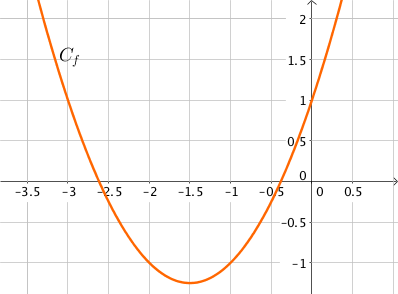
On souhaite étudier les variations de la fonction $f$.
La dérivée de la fonction $f$ est $f'(x) = 2x + 3$.
On étudie le signe de
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
