L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
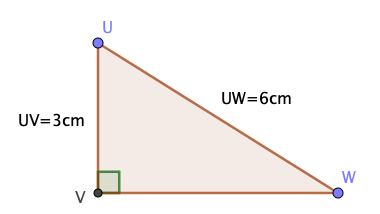
$\cos(\widehat{VUW})=\dfrac{hypotenuse}{adjacent}$
$\cos(\widehat{VUW})=\dfrac{adjacent}{hypotenuse}$
$\sin(\widehat{VUW})=\dfrac{adjacent}{hypotenuse}$
$\tan(\widehat{VUW})=\dfrac{oppose}{hypotenuse}$
Retenir le moyen mnémotechnique : CAH SOH TOA
Ce sont des propriétés de cours. Les retenir grâce au moyen mnémotechnique suivant : CAH SOH TOA
CAH : $\cos(\widehat{VUW})=\dfrac{adjacent}{hypotenuse}$
SOH : $\sin(\widehat{VUW})=\dfrac{oppose}{hypotenuse}$
TOA : $\tan(\widehat{VUW})=\dfrac{oppose}{adjacent}$
Question 2

$\cos(\widehat{VUW})=0,5$
$\cos(\widehat{VUW})=0,2$
$\sin(\widehat{VUW})=0,84$
$\sin(\widehat{VUW})=0,65$
Ce sont des propriétés de cours. Les retenir grâce au moyen mnémotechnique suivant : CAH SOH TOA
CAH : $\cos(\widehat{VUW})=\dfrac{adjacent}{hypotenuse}$
SOH : $\sin(\widehat{VUW})=\dfrac{oppose}{hypotenuse}$
TOA : $\tan(\widehat{VUW})=\dfrac{oppose}{adjacent}$
$\cos(\widehat{VUW})=\dfrac{VU}{UW}=\dfrac{3}{6}=0,5$
Question 3

$\tan(\widehat{UWV})=0,6$
$\tan(\widehat{UWV})=0,4$
$\sin(\widehat{UWV})=0,3$
$\sin(\widehat{UWV})=0,5$
Attention on ne cherche pas la valeur de l<angle dans cette question mais bien la valeur du sinus ou de la tangeante de l'angle. Ne pas confondre
Ce sont des propriétés de cours. Les retenir grâce au moyen mnémotechnique suivant : CAH SOH TOA
CAH : $\cos(\widehat{UWV})=\dfrac{adjacent}{hypotenuse}$
SOH : $\sin(\widehat{UWV})=\dfrac{oppose}{hypotenuse}$
TOA : $\tan(\widehat{UWV})=\dfrac{oppose}{adjacent}$
$\sin(\widehat{UWV})=\dfrac{VU}{UW}=\dfrac{3}{6}=0,5$
Question 4
Quelle est la mesure de l'angle $\widehat{VUW}$ ?

$30^{\circ}$
$45^{\circ}$
$60^{\circ}$
$70^{\circ}$
On sait d'après la question 2 que :
$\cos(\widehat{VUW})=\dfrac{VU}{UW}=\dfrac{3}{6}=0,5$
Avec la calculatrice en appuyant sur la touche $cos^{-1}$ on note que
$\widehat{VUW}=cos^{-1}(0,5)=60°$
Question 5
Quelle est la mesure de l'angle $\widehat{UWV}$ ?

$50^{\circ}$
$20^{\circ}$
$30^{\circ}$
$40^{\circ}$
On sait d'après la question 3 que :
$\sin(\widehat{UWV})=\dfrac{VU}{UW}=\dfrac{3}{6}=0,5$
Avec la calculatrice en appuyant sur la touche $sin^{-1}$ on note que $\widehat{UWV}=sin^{-1}(0,5)=30°$
