L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Dans le triangle rectangle \(ABC\), que vaut le cosinus de \( \widehat{ABC}\) ?
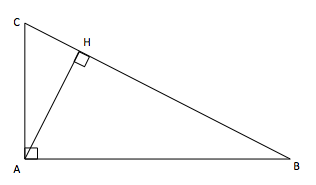
\(\cos( \widehat{ABC})\) = \( \dfrac{BH}{AB}\)
\(\cos( \widehat{ABC})\) = \( \dfrac{BC}{AB}\)
\(\cos (\widehat{ABC})\) = \( \dfrac{AB}{BC}\)
\(\cos(\widehat{ABC})\) = \( \dfrac{AC}{BC}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Par exemple, cosinus = \( \dfrac{\text{côté adjacent}}{\text{hypoténuse}}\)
Question 2
Que vaut le cosinus de \( \widehat{ABH}\) ?
\(\cos ( \widehat{ABH})=\dfrac{BH}{AB}\)
\(\cos ( \widehat{ABH})= \dfrac{BH}{AH}\)
\(\cos ( \widehat{ABH})=\dfrac{AB}{BH}\)
\(\cos ( \widehat{ABH})=\dfrac{AB}{BC}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Par exemple, cosinus = \( \dfrac{\text{côté adjacent}}{\text{hypoténuse}}\)
Question 3
Que vaut le sinus de \( \widehat{ABC}\) ?
\(\sin (\widehat{ABC})=\dfrac{AH}{AB}\)
\(\sin (\widehat{ABC})= \dfrac{CA}{CB}\)
\(\sin (\widehat{ABC})= \dfrac{AB}{BC}\)
\(\sin (\widehat{ABC})=\dfrac{BC}{AC}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Question 4
Que vaut le sinus de \( \widehat{ABH}\) ?
\(\sin ( \widehat{ABH})= \dfrac{AH}{BH}\)
\(\sin (\widehat{ABH})=\dfrac{HB}{AB}\)
\(\sin (\widehat{ABH})=\dfrac{AB}{AH}\)
\(\sin (\widehat{ABH})= \dfrac{HA}{AB}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Question 5
Que vaut la tangente de \( \widehat{ABC}\) ?
\(\tan( \widehat{ABC})=\dfrac{CA}{AB}\)
\(\tan( \widehat{ABC})=\dfrac{BC}{AC}\)
\(\tan( \widehat{ABC})= \dfrac{AC}{BC}\)
\(\tan( \widehat{ABC})= \dfrac{AB}{BC}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Question 6
Dans le triangle rectangle \(ABH\), que vaut la tangente de \( \widehat{ABH}\) ?
\(\tan( \widehat{ABH})= \dfrac{HB}{AB}\)
\(\tan( \widehat{ABH})= \dfrac{AH}{HB}\)
\(\tan( \widehat{ABH})=\dfrac{AH}{AB}\)
\(\tan( \widehat{ABH})= \dfrac{BH}{AH}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C'est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente.
Question 7
Dans le triangle rectangle \(ABC\), on admet que \(\cos( \widehat{B})= 0,8\).
Quelle relation peut vous permettre de calculer \(\sin(\widehat{B})\) ?
\( \dfrac{\cos( \widehat{B})}{\sin (\widehat{B})}= 1\)
\(\cos( \widehat{B}) + \sin( \widehat{B}) = 1\)
\(\cos^2( \widehat{B}) - \sin^2( \widehat{B}) = 1\)
\(\cos^2( \widehat{B}) + \sin^2( \widehat{B}) = 1\)
Cette relation est à connaître par cœur.
Elle dérive directement du théorème de Pythagore appliqué au triangle rectangle.
Question 8
\(\cos^2( \widehat{B}) + \sin^2( \widehat{B}) = 1\), par conséquent, que vaut \(\sin^2 (\widehat{B})\) ?
\(\sin^2 (\widehat{B}) = \cos^2 (\widehat{B}) - 1= 0,8^2 - 1 = 0,64 - 1 = - 0,36\)
\(\sin^2 (\widehat{B}) = 1 - \cos (\widehat{B} )= 1 - 0,8 = 1 - 0,8 = 0,2\)
\(\sin^2( \widehat{B}) = 1 - \cos^2( \widehat{B}) = 1 - 0,8^2 = 1 - 0,64 = 0,36\)
\(\sin^2 (\widehat{B}) = 1 + \cos^2 (\widehat{B}) = 1 + 0,8^2 = 1 + 0,64 = 1,64\)
Pour isoler \(sin^2 \widehat{B}\), il faut soustraire \(cos^2 \widehat{B}\) à chaque membre de l’égalité.
Question 9
\(\sin^2 (\widehat{B}) = 0,36\), par conséquent, que vaut \(\sin (\widehat{B})\) ?
\(\sin (\widehat{B}) = \sqrt{0,36} = 0,6 \)
\(\sin (\widehat{B}) = 0,36\)
\(\sin (\widehat{B}) = \dfrac{0,36}{2} = 0,18\)
\(\sin (\widehat{B}) = \sqrt{0,36} = 0,06 \)
Vous connaissez le carré de \(sin \widehat{B}\), or c’est un nombre positif, vous cherchez donc la racine carrée de $0,36$.
Question 10
On a : \(\cos (\widehat{B}) = 0,8\) et \(\sin (\widehat{B}) = 0,6\).
Que vaut \(\tan (\widehat{B})\)?
\(\tan (\widehat{B} )= \sin (\widehat{B}) + \cos (\widehat{B}) = 0,6 + 0,8 = 1,4\)
\(\tan (\widehat{B}) = \sin (\widehat{B}) \times \cos (\widehat{B} )= 0,6 \times 0,8 = 0,48\)
\(\tan( \widehat{B}) = \dfrac{\cos(\widehat{B})}{\sin(\widehat{B})} = \dfrac{0,8}{0,6} \approx 1,33\)
\(\tan( \widehat{B}) = \dfrac{\sin(\widehat{B})}{\cos(\widehat{B})}= \dfrac{0,6}{0,8} = 0,75\)
Là aussi, c’est à savoir par cœur : \(\tan( \widehat{B}) = \dfrac{\sin(\widehat{B})}{\cos(\widehat{B})}\)
C'est une valeur à calculer mentalement. On vérifie que $0,6^2=0,36$