Prendre une feuille et un stylo et répondre aux questions suivantes.
On considère le verre ci-dessous, ayant la forme d'un cône de révolution, de hauteur $OS = 12 \ cm$ et de rayon $OA = 3 \ cm$.
Léa veut fêter son anniversaire et inviter 10 amis. Elle a préparé deux litres de jus de fruits et a acheté des verres tous identiques à celui représenté ci-contre.
1) Montrer que le volume de ce verre (en $cm^3$) est égal à $36 \pi$.
2) Si Léa remplit entièrement les verres, combien pourra-t-elle en remplir ?
3) Léa décide alors de ne remplir les verres qu’au $\dfrac{5}{6}$ de leur hauteur et pense qu’elle pourra servir au moins 3 verres à chacun.
A-t-elle raison ? Justifier votre réponse.
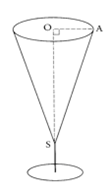
1) Soit $V$ le volume de ce verre conique :
$V = \dfrac{Aire de la base \times hauteur}{3} $
$V= \dfrac{\pi \times OA^2 \times OS}{3} $
$V= \dfrac{\pi \times 3^2 \times 12}{3} $
$V= 36 \pi \ cm^3$
2) 2 litres de jus de fruits correspondent à $2000 \ cm^3$ et un verre a un volume de $36 \pi \ cm^3$.
Or $\dfrac{2000}{36 \pi} \approx 17.7$
Ainsi Léa peut remplir entièrement $17$ verres.
3) Si on remplit un verre aux $\dfrac{5}{6}$ de sa hauteur alors le volume sera
$V' = V \times \left(\dfrac{5}{6}\right)^3 $
$V'= \dfrac{36 \pi \times 5^3}{6^3} $
$V'\approx 65 cm^3$
Or $\dfrac{2000}{\dfrac{36 \pi \times 5^3}{6^3}} \approx 30.6$.
Elle pourra donc servir $30$ verres.
Léa avec ses amis sont au nombre de $11$, or $3 \times 11 = 33$.
Ainsi, tous n’auront pas $3$ verres.
