L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Pour toutes les questions, on considère la figure ci-dessous.
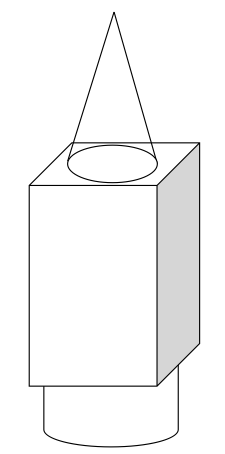
La fusée DNB2017 est constituée de 3 parties distinctes :
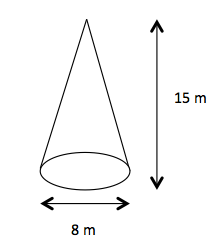
- Partie du haut : la coiffe.
Un cône de hauteur 15m et de disque de base de diamètre 8m.
- Partie intermédiaire : l’habitacle.
Un parallélépipède rectangle de côtés 10 m, 10 m et 50 m.

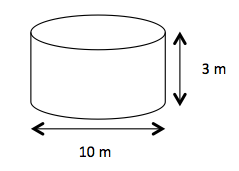
- Partie basse : le moteur.
Un cylindre de hauteur 3m et de disque de base de diamètre 10m.
Tu as obtenu le score de
Question 1
Quelle formule va permettre de calculer l'aire du disque de la base du cône (la coiffe) ?
Aire = \( \pi \times d\)
Aire = \( \pi \times d^2\)
Aire = \( \pi \times R^2\)
Aire = \( 2 \times \pi \times R\)
Allez ! Un effort ! C’est si loin que ça la 6ème ?
Il faut un carré … pour calculer l’aire.
Question 2
La formule de l'aire d'un disque de rayon \(R\) étant Aire = \( \pi \times R^2\).
Quel est l'arrondi au dixième de l'aire de ce disque ?
Aire \( \approx \) 50,2 m2
Aire \( \approx \) 50,3 m2
Aire \( \approx \) 50,26 m2
Aire \( \approx \) 201 m2
Aire \( \approx \) 201,06 m2
N’oubliez pas que le rayon … c’est la moitié du diamètre ! ;-)
Le chiffre des « dixièmes » c’est le premier à droite de la virgule.
Question 3
On veut calculer l'aire totale de la partie habitable (parallélépipède rectangle).
Quel calcul doit-on effectuer ?
Aire = 10 × 10 × 50
Aire = 10 × 50 × 50
Aire = 2 × 10 × 10 + 4 × 50 × 50
Aire = 2 × 10 × 10 + 4 × 10 × 50
Un parallélépipède rectangle a 6 faces rectangulaires.
Dans notre cas particulier, 2 de ces faces sont des carrées.
Question 4
L'aire totale est donc égale à 2 × 10 × 10 + 4 × 10 × 50
Combien vaut cette aire ?
Aire = 1 200 m2
Aire = 400 000 m2
Aire = 2 000 m2
Aire = 2 200 m2
Attention à la priorité des opérations.
Prenez soin de choisir la bonne unité.
Question 5
Quelle formule va permettre de calculer l'aire du disque de la base du cylindre (le moteur) ?
Aire = \(\pi \times d\)
Aire = \(\pi \times d^2\)
Aire = \(\pi \times R^2\)
Aire = \(2 \times \pi \times r\)
Allons ! Vous l'avez fait dans la première question !
Question 6
Nous avons déjà vu dans la question 1) que la formule de l'aire dun disque de rayon \(R\) est Aire = \( \pi \times R^2\)
Quel est l'arrondi au centième de l'aire de ce disque ?
Aire \(\approx 78,6 \ m^2\)
Aire \(\approx 78,5 \ m^2\)
Aire \(\approx 78,53 \ m^2\)
Aire \(\approx 78,54 \ m^2\)
N’oubliez pas que le rayon … c’est la moitié du diamètre ! ;-)
Le chiffre des « centièmes » c’est le deuxième à droite de la virgule.
Question 7
On veut calculer l'aire « latérale » du cylindre (le moteur). Quelle figure est le patron de cette aire latérale ?
Un carré.
Un rectangle.
Un cercle.
Un disque.
Imaginez que vous découpez le cylindre et que vous mettez tout à plat.
Question 8
La face « latérale » du cylindre (le moteur) ayant pour patron un rectangle, quelle est la largeur de ce rectangle ?
$3$ m
$10$ m
$5$ m
$8$ m
La largeur de ce rectangle est la hauteur du cylindre.
Question 9
La face « latérale » du cylindre (le moteur) ayant pour patron un rectangle.
On veut déterminer la longueur de ce rectangle.
Cette longueur est, en fait, la longueur du disque de base.
Quelle formule va-t-on utiliser ici pour calculer cette longueur ?
Longueur = \( \pi \times d^2\)
Longueur = \(2 \times \pi \times d\)
Longueur = \(2 \times \pi \times R\)
Longueur = \( \pi \times R\)
Formule de la longueur d’un cercle de rayon \(R\)… Back to the 6ème !
Deux pierres ;-)
Question 10
On a donc Longueur = \(2 \times \pi \times R\)
Quel est l'arrondi au centième de cette longueur ?
Longueur \( \approx 31,41 \ m\)
Longueur \( \approx 31,42 \ m\)
Longueur \( \approx 62,83 \ m\)
Longueur \( \approx 31,4 \ m\)
N’oubliez pas que le rayon … c’est la moitié du diamètre ! ;-)
Le chiffre des « centièmes » c’est le deuxième à droite de la virgule.
Question 11
Pour terminer, le patron de l'aire latérale du cylindre (moteur) étant un rectangle de largeur 3 m et de longueur environ 31,42 m.
Quel est l'arrondi au centième de son aire ?
Aire \(\approx 94,25 \ m^2\)
Aire \(\approx 94,3 \ m^2\)
Aire \(\approx 94,26 \ m^2\)
Aire \(\approx 94,2 \ m^2\)
L’aire d’un rectangle de longueur L et de largeur l est donnée par la formule : Aire = L × l
Le chiffre des « centièmes » c’est le deuxième à droite de la virgule.
