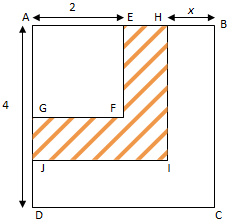
L'énoncé
Dans la figure ci-contre, \(AEFG\), \(AHIJ\) et \(ABCD\) sont des carrés.
Question 1
Calculer \(AH\) en fonction de \(x\).
On soustrait la petite distance à la grande :
\(AH = AB -HB = 4 - x\)
\(ABCD\) est un carré donc \(AB = AD = 4\).
\(AH = AB – HB\)
Question 2
Grâce à votre réponse précédente, déduisez-en l'aire de \(AHIJ\).
\(AHIJ\) est un carré de côté \(AH\) dont on sait depuis le 1) qu'il vaut \(4 -x\)
Donc Aire \(AHIJ = (4 -x)^2\)
L’aire d’un carré de côté \(c\) est \(c^2\).
Or \(AH = 4 - x\)
Question 3
Grâce à votre réponse précédente, déduisez-en l'aire de la partie hachurée.
Soit $A$ l'aire de partie hachurée
\(A=\) Aire \(AHIJ\) -Aire \(AEFG\)
\(A=(4 -x)^2 - 2^2\)
\(A=(4 -x)^2 - 4\)
L’aire que vous cherchez peut se trouver par une soustraction.
Aire \(AHIJ = (4-x)^2\) et Aire \(AEFG = 2^2\)
Question 4
Développez et réduisez l'expression \(M = (4 -x)^2 - 4\)
\(M = (4 -x)^2 - 4 \)
\(M = (4 -x)(4-x) - 4 \)
\(M = 16 -4x-4x + x^2 - 4\)
\(M = x^2 - 8x + 12\)
Ne jamais oublier les identités remarquables.
\((a-b)^2 = a^2 - 2ab + b^2\)
Question 5
Vérifier que \(M =(2 -x)(6 -x) =(4 -x)^2 - 4\)
On a: $(2 -x)(6 -x) =12-2x-6x+x^2=x^2-8x+12$ ce qui est le résultat de l'expression précédente.
On a bien vérifié que \(M =(2 -x)(6 -x) =(4 -x)^2 - 4\)
Developper les deux expressions
Question 6
Grâce à votre réponse précédente, calculez \(M\) lorsque \(x = 2\)
\(M = (2 -x)(6 -x)\)
\(M = (2 -2)(6 -2)\)
\(M = 0 \times 4\)
\(M = 0\)
Quelle expression de \(M\) est-elle la plus simple à utiliser dans notre cas ?
Regardez bien la forme factorisée.
Question 7
Que traduit ce résultat pour la figure ?
Lorsque \(x = 2\), \(AE = 2\) et \(HB = 2\) aussi.
Or \(AB = 4\) ce qui signifie que \(EH = 0\) !
Par conséquent la partie hachurée est « écrasée », ce qui est cohérent avec le calcul de la question 6.
L'aire de cette partie est nulle.
Regardez bien la figure, \(x\) maintenant vaut 2.
\(AB = 4\) mais \(AE = 2\) et \(HB = 2\).