Fiche de cours
Étape 3 : les coordonnées du vecteur vitesse
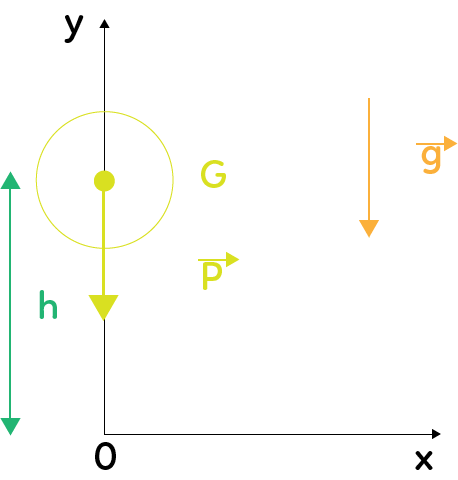
Il a été trouvé précédemment, en primitivant les coordonnées du vecteur accélération, que $\overrightarrow{v}$ s’écrit sous la forme :
$ \left\{
\begin{array}{ccc}
v_x & = & C_1 \\
v_y & = & -gt + C_2 \\
\end{array}
\right.$
Il s’agit donc de déterminer totalement la vitesse en trouvant la valeur des constantes grâce aux conditions initiales, c’est-à-dire au moment où on lâche la balle à $t = 0$. A $t = 0$, la balle n’avait pas de vitesse initiale, ainsi, $\overrightarrow{v}(t = 0) = \overrightarrow{0}$; il faudra faire attention à écrire une égalité vectorielle.
Or en se plaçant à $t = 0$ s et en remplaçant donc $t$ par $0$ dans les coordonnées de la vitesse on obtient une nouvelle information sur $\overrightarrow{v}(t = 0)$ qui est alors égal à $ \left\{
\begin{array}{ccccc}
v_x & = &
