Le plan complexe est muni d'un repère orthonormé $(O,\vec{u};\vec{v})$.
$f$ est l'application qui fait correspondre à tout point $M$ d'affixe $z$ différente de $-3$, le point $M'$ d'affixe : $\dfrac{1}{z+3}$
On pourra noter $f(M) = M'$ avec $M(z)$ et $M' \left( { \dfrac{1}{z+3} } \right)$
L'application $f$ conserve l'alignement des points ? C'est à cette question que nous allons répondre.
1) Soient $A$, $B$ et $C$ les points d'affixes respectives :
$z_A = - \dfrac {5}{2}$; $z_B = - \dfrac{5}{2} + i$; $z_C = - \dfrac{5}{2} - \dfrac{1}{2} i$
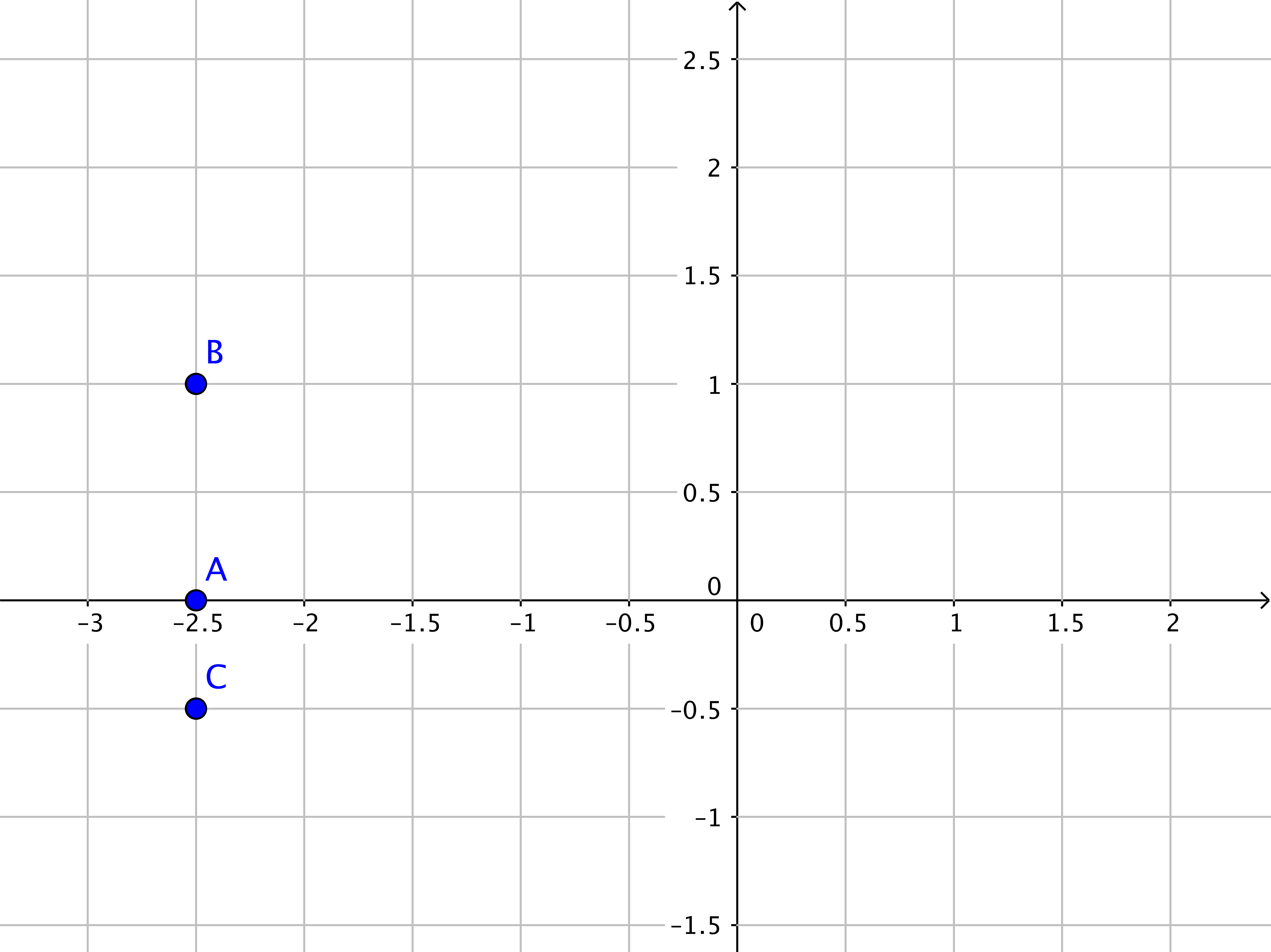
a) Placer les points $A$, $B$ et $C$ sur un graphique. On prendra 2 cm par unité graphique.
b) Calculer les affixes $A'$, $B'$ et $C'$, images respectives de $A$, $B$ et $C$ par $f$ puis placer les points sur le graphique.
c) Démontrer que $A'$, $B'$ et $C'$ ne sont pas alignés.
2) L'application $f$ conserve-t-elle l'alignement des points ? Répondez à l'aide des questions précédentes ?
1) a) Placer les points $A$, $B$ et $C$ :
b) $Z_{A'} = \dfrac{1}{Z_A +3} = \dfrac{1}{-\frac{5}{2} + 3} = \dfrac{1}{\frac{1}{2}} = 2$
$Z_{B'} = \dfrac{1}{Z_B +3} = \dfrac{1}{-\frac{5}{2} + i + 3} = \dfrac{2}{1+ 2i} = \dfrac {2(1-2i)}{(1+2i)(1-2i)} = \dfrac{2-4i}{1^2 + 2^2} = \dfrac{2}{5} - \dfrac{4}{5}i$
$Z_{C'} = \dfrac{1}{Z_C +3} = \dfrac{1}{-\frac{5}{2} -\frac{1}{2} i +3} = \dfrac{2}{1-i} = \dfrac{2(1+i)}{(1-i)(1+i)} = \dfrac{2(1+i)}{1^2 + (-1)^2} = 1 + i$
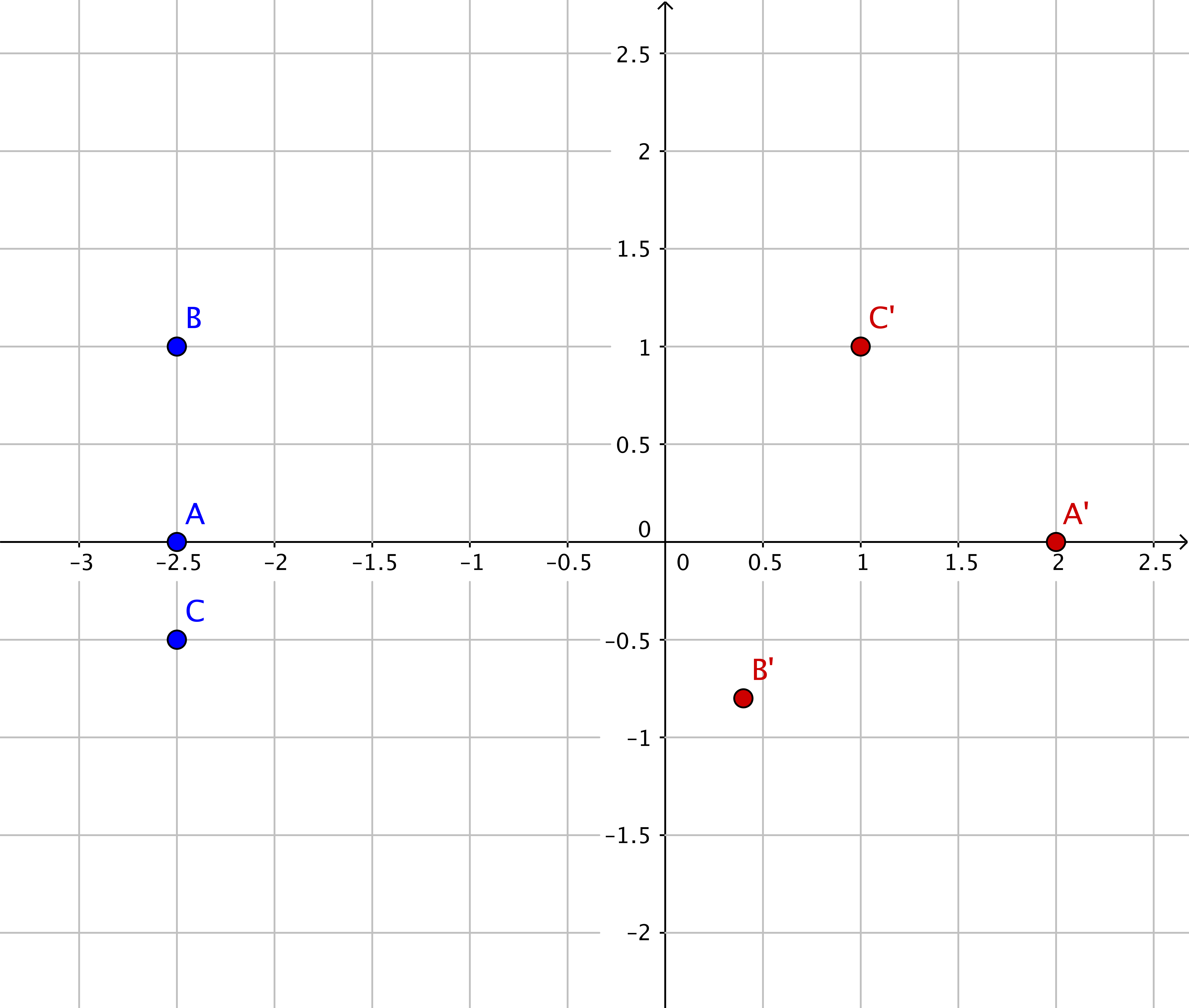
c) $A'$, $B'$ et $C'$ sont alignés si et seulement si le déterminant des vecteurs $\vec{A'B'}$ et $\vec {A'C'}$ est nul.
Calculons les coordonnées des vecteurs $\vec{A'B'}$ et $\vec{A'C'}$ :
$\vec{A'B'} \left( {-\dfrac{8}{5} ; - \dfrac{4}{5}} \right)$
$\vec{A'C'} (-1;1)$
$xy' - x'y = \left( {-\dfrac{8}{5}} \right) \times 1 - (-1) \times \left( {-\dfrac{4}{5}} \right) = - \dfrac{8}{5} - \dfrac{4}{5} = - \dfrac{12}{5}\ne 0$
Les points $A'$, $B'$ et $C'$ ne sont pas alignés.
2) On sait que $A'$, $B'$ et $C'$ ne sont pas alignés. Vérifions si $A$, $B$ et $C$ sont alignés.
$\vec{AB} (0;1)$
$\vec{AC} \left( {0; - \dfrac{1}{2}} \right)$
$xy' - x'y = 0 \times \dfrac{1}{2} - 0 \times 1 = 0 -0 = 0$
Donc $A$, $B$ et $C$ sont alignés.
On pouvait aussi remarquer que les affixes avaient la même partie réelle.
Comme $A$, $B$ et $C$ sont alignés et que $A'$, $B'$ et $C'$ ne sont pas alignés, alors cela nous permet de conclure que l'application $f$ ne conserve pas l'alignement.
