Le plan complexe est muni d'un repère orthonormé $(O; \vec{u};\vec{v})$.
On donne : $A(-1+2i)$ ; $B(-2-i)$
1) Placer les points $A$ et $B$ sur le graphique.
2) a) Calculer $\dfrac{b}{a}$.
b) Déterminer le module et un argument de $\dfrac{b}{a}$.
c) On admet que $arg\left( {\dfrac{b}{a}}\right) = arg (b) - arg (a) [2\pi]$.
Montrer que $(\vec{OA},\vec{OB}) =arg\left( {\dfrac{b}{a} }\right) [2\pi]$.
d) En déduire la nature du triangle $OAB$.
1) $A(-1+2i)$ ; $B(-2-i)$
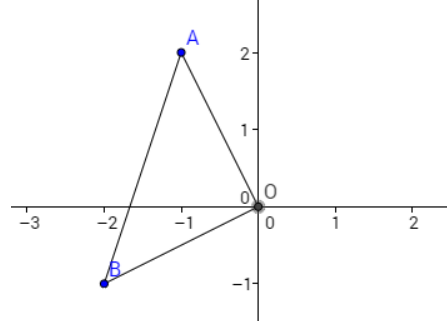
2) a) $\dfrac{b}{a} =\dfrac{-2-i}{-1+2i} =\dfrac{i(-1+2i)}{-1+2i} = i$
b) On en déduit que $\left\lvert \dfrac{b}{a}\right\lvert =\lvert i\lvert = 1$
Et $arg\left( {\dfrac{b}{a} }\right) = arg (i) = arg\left( {\cos\left( {\dfrac{\pi}{2}}\right) + i\sin\left({\dfrac{\pi}{2}}\right) }\right)=\dfrac{\pi}{2} [2\pi]$
c) Montrons que $arg\left( {\dfrac{b}{a} }\right) = (\vec{OA},\vec{OB}) [2\pi]$
On sait d'après la somme d'angles orientés que $(\vec{OA},\vec{OB}) = (\vec{OA},\vec{u}) + (\vec{u},\vec{OB}) [2\pi]$
Ainsi : $(\vec{OA},\vec{OB}) = - (\vec{u},\vec{OA}) + (\vec{u},\vec{OB}) [2\pi]$ soit :
$(\vec{OA},\vec{OB}) = (\vec{u},\vec{OB}) - (\vec{u},\vec{OA})[2\pi]$
$(\vec{OA},\vec{OB}) = arg(b) - arg(a)[2\pi]$
$(\vec{OA},\vec{OB}) = arg\left({\dfrac{b}{a} }\right) [2\pi]$
d) Déduire la nature du triangle $OAB$.
On vient de montrer que : $\arg\left({\dfrac{b}{a} }\right) = (\vec{OA},\vec{OB}) [2\pi]$
Ainsi, $(\vec{OA},\vec{OB}) =\dfrac{\pi}{2} [2\pi]$
Et $\left\lvert \dfrac{b}{a} \right\lvert =\dfrac{OB}{OA} = 1$ soit $OB = OA$
Alors le triangle est isocèle et rectangle en $O$.
