L'énoncé
On considère l’application \(f\) du plan dans lui même qui à tout point \(M\), d’affixe \(z\) distincte de \(2i\), associe le point \(M'\) d’affixe : \(z' = \dfrac{z+i}{z-2i}\)
Question 1
Pour \(z \neq 2i\), on pose \(z=2i+re^{i\theta}\), avec \(r>0\) et \(\theta \in \mathbb{R}\).
Ecrire \(z'-1\) à l'aide de \(r\) et \(\theta\).
Pour tout \(z \neq 2i\), on calcule :
\(z'-1 = \dfrac{z+i}{z-2i}-1\)
\(z'-1 = \dfrac{z+i}{z-2i}-\dfrac{z-2i}{z-2i}\)
\(z'-1 = \dfrac{3i}{z-2i}\) Si on pose : \(z=2i+re^{i\theta}\), avec \(r>0\) et \(\theta \in \mathbb{R}\), alors :
\(z'-1 = \dfrac{3i}{z-2i}\)
Ainsi : \(z'-1 = \dfrac{3i}{2i+re^{i\theta}-2i}\)
\(z'-1 = \dfrac{3i}{re^{i\theta}}\)
\(z'-1 = \dfrac{3i}{r}e^{-i\theta} \)
Enfin, on peut écrire :
\(z'-1 = \dfrac{3i}{r}e^{-i\theta}\)
\(z'-1 = \dfrac{3}{r}e^{i\frac{\pi}{2}}e^{-i\theta}\) \(z'-1 = \dfrac{3}{r}e^{i\left( \frac{\pi}{2}-\theta\right)}\)
Ecrire \(z'-1\) en fonction de \(z\) puis remplacez \(z\) par \(z = 2i + re^{i\theta}\)
Rappel : \(\frac{1}{e^{i\theta}} = e^{-i\theta}\)
Oubli fréquent des élèves : \(i = e^{i \frac{\pi}{2}}\) (vérifiez sur une figure si vous avez un doute)
Question 2
$A$ est le point d'affixe \(2i\).
Déterminer l'ensemble \(E_1\) des points \(M\) pour lesquels \(|z'-1|=3\)
Un point \(M\) aura une affixe \(z\) vérifiant \(|z'-1|=3\) si et seulement si :
\(\left| \dfrac{3}{r}e^{i\left( \frac{\pi}{2}-\theta\right)} \right| = 3\)
\(\Leftrightarrow \left| \dfrac{3}{r} \right|\left| e^{i\left( \frac{\pi}{2}-\theta \right)} \right| =3\)
\(\Leftrightarrow \dfrac{3}{r}= 3 \) \(\Leftrightarrow \dfrac{1}{r} = 1 \)
\(\Leftrightarrow r=1\)
Ainsi on aura : \(z = z_A+e^{i\theta} \Leftrightarrow z - z_A = e^{i\theta}\)
Ce qui implique :
\(|z-z_A| = |e^{i\theta}| = 1 \Leftrightarrow AM = 1\)
et :
\(arg(z-z_A)=\theta(2\pi)\)
Le point \(M\) appartient donc au cercle de centre \(A\) et de rayon 1.
\(E_1\) est donc le cercle de centre \(A\) et de rayon 1.
Utilisez bien sur la question précédente.
Souvenez-vous que les complexes de la forme \(e^{i\theta}\) sont de module 1 donc vous en déduirez une condition sur \(r\).
Pensez alors à rechercher dans votre cours l'écriture complexe de l'affixe d'un point qui appartient à un cercle de centre et de rayon donné.
Question 3
Déterminer l'ensemble \(E_2\) des points \(M\) pour lesquels \(arg(z'-1)= \dfrac{\pi}{4}(2\pi)\)
Puisque \(z'-1 = \dfrac{3}{r}e^{i\left( \frac{\pi}{2}-\theta \right)}\) On aura :
\(arg(z'-1) = \dfrac{\pi}{4}(2\pi)\)
Si et seulement si : \( \dfrac{\pi}{2}- \theta = \dfrac{\pi}{4}(2\pi) \Leftrightarrow \theta = \dfrac{\pi}{4}(2\pi) \)
Ainsi, \(z-z_A = \dfrac{3}{r}e^{i\frac{\pi}{4}}\), donc en traduisant en termes d'arguments :
\((\widehat{\overrightarrow{u}; \overrightarrow{AM}}) = \dfrac{\pi}{4}(2\pi)\)
Le point \(M\) appartient donc à la demi-droite d'origine \(A\) et d'équation polaire \(\theta = \dfrac{\pi}{4}(2\pi)\)
\(E_2\) est donc la demi-droite d'origine $A$ et d'équation polaire \(\theta = \dfrac{\pi}{4} (2\pi )\)
Attention, deux arguments sont toujours égaux modulo \(2\pi\).
Ainsi, montrez que \(\dfrac{\pi}{2}-\theta= \dfrac{\pi}{4}\) modulo \(2\pi\). Vous en déduirez \(\theta\).
L'argument de l'affixe de \(\overrightarrow{AM}\) est par définition la mesure de \((\widehat{\overrightarrow{u}; \overrightarrow{AM}})\) Recherchez alors une figure géométrique dont les points forment un angle constant avec l'axe des réels...
Question 4
Représenter les ensembles \(E_1\) et \(E_2\)
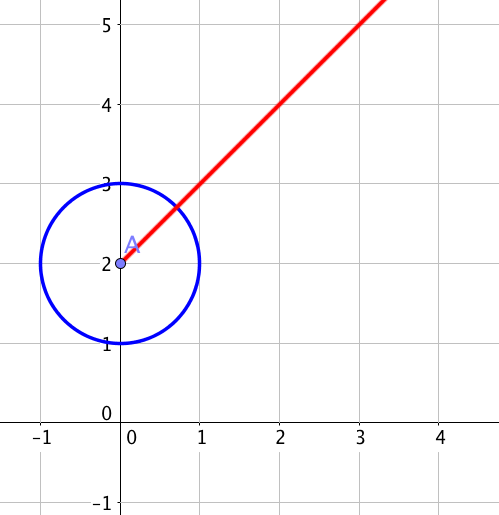
Vous n'avez qu'à tracer en choisissant une unité assez grande.
