L'énoncé
Question 1
Vérifier que \(a^5 = 1\).
\(a^5 = e^{5i\frac{2\pi}{5}} = e^{2i\pi} = 1\)
Question 2
Vérifier que, pour tout \(z\) complexe : \(z^5-1=(z-1)(1+z+z^2+z^3+z^4)\)
On développe le membre de droite et on obtient celui de gauche.
Question 3
En déduire que \(1 + a + a^2 + a^3 + a^4 = 0\).
Comme \(a^5 = 1\), \(a\) est une solution de l'équation \(z^5=1\)
Ou encore de \(z^5-1=0\)
C'est à dire de \((z-1)(1+z+z^2+z^3+z^4)=0\).
Mais comme \(a\) ne vaut pas 1, \(a\) est solution de \(1+z+z^2+z^3+z^4=0\)
Il est donc tel que \(1 + a + a^2 + a^3 + a^4 = 0\).
Question 4
Montrer que \(a^3 = \overline{a}^2\) et que \(a^4 = \overline{a}\).
\(a^3 = \left( e^{i\frac{2\pi}{5}} \right)^3 = e^{i\frac{6\pi}{5}}\)
\(\overline{a}^2 = \left( e^{-i\frac{2\pi}{5}} \right)^2 = e^{-i\frac{4\pi}{5}} = e^{2i\pi-i\frac{4\pi}{5}} = e^{i\frac{6\pi}{5}} \)
Même chose pour \(a^4 = \overline{a}\).
Rappelez vous que \(\overline{e^{i\theta}} = e^{-i\theta}\)
Question 5
Dans \(1+a+a^2+a^3+a^4=0\), on a donc :
\( 1+a+a^2+\overline{a}^2+\overline{a} = 0\)
Or \((a+\overline{a})^2 = a^2+ 2a\overline{a}+\overline{a}^2 = a^2+2+\overline{a}^2\).
Ainsi \((a+\overline{a})^2+(a+\overline{a})-1=0\).
Question 6
Résoudre, dans \(\mathbb{R}\), l'équation \(4x^2 + 2x -1 = 0\).
On calcule le discriminant : $\Delta = 20>0$
Les solutions sont donc : \(x_1 = \dfrac{-1-\sqrt{5}}{4}\) et \(x_2 = \dfrac{-1+\sqrt{5}}{4}\)
Question 7
Calculer \((a+\overline{a})\) à l'aide de la formule d'Euler et en déduire la valeur exacte de \(\cos\left( \frac{2\pi}{5} \right)\) .
\((a+\overline{a}) = e^{i\frac{2\pi}{5}}+e^{-i\frac{2\pi}{5}} = 2\cos\left( \frac{2\pi}{5} \right)\) d'après la formule d'Euler.
Ainsi, en remplaçant dans \((a+\overline{a})^2+(a+\overline{a})-1=0\),
On a : \((2\cos \left( \frac{2\pi}{5} \right))^2+(2\cos \left( \frac{2\pi}{5} \right))-1=0\)
\( \Leftrightarrow 4 \cos^2\left( \frac{2\pi}{5} \right)+2\cos\left( \frac{2\pi}{5} \right)-1=0 \)
\(\cos\left( \frac{2\pi}{5} \right)\) est donc une des deux solutions de l'équation de la question précédente.
Comme ce nombre est forcément positif \((\dfrac{2\pi}{5}=72°<90)\),
Il vaut : \(\cos\left( \frac{2\pi}{5} \right)=\dfrac{-1+\sqrt{5}}{4}\)
Faites le lien entre les solutions de l’équation précédente et la valeur de \(cos\left( \frac{2\pi}{5} \right)\)
Question 8
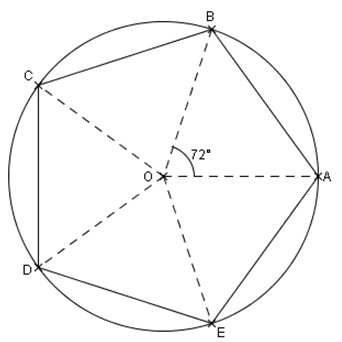
Placer les points \(A\), \(B\), \(C\) , \(D\) et \(E\) d'affixes respectifs : \( 1 ; a ; a^2 ; a^3 \text{ et } a^4 \) dans le plan complexe.
On trace un cercle de rayon 1 et on place les points pour former un pentagone régulier.
On a : \(\dfrac{360°}{5}=72°\)
Les points ont des affixes de module 1 donc tous sur un même cercle. Relisez le titre et vérifiez que vous avez obtenu la figure recherchée.