Fiche de cours
Réciproque d'une fonction
Définition :
Soit $f$ une fonction continue et strictement monotone (strictement croissante ou strictement décroissante) sur un intervalle,
On appelle fonction réciproque de $f$, la fonction $g$ telle que :
$g(f(x)) = f(g(x)) = x$.
Les courbes des deux fonctions sont symétriques par rapport à la droite d'équation $y = x$.
Exemples :
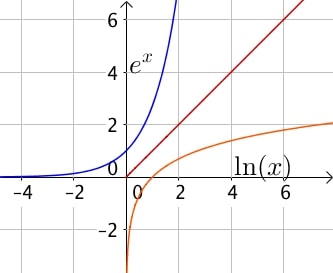
Pour $x > 0$, $e^{\ln(x)}=\ln(e^x) = x$.
Graphiquement, on remarque que les courbes sont symétrique par rapport à la droite d'équation $y = x$.
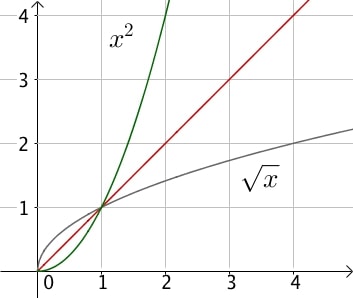
Pour $x \geq 0$, $\sqrt{x^2} = (\sqrt{x})^2 = x$.
On observe à nouveau la propriété de symétrie.
Exercice :
Déterminer la fonction réciproque de $f$ définie sur $\mathbb{R}$ par $f(x) = -2x + 3$
$f$ est une fonction affine qui est strictement décroissante. En outre $f$ est continue.
La méthode consiste à poser $y = f(
