L'énoncé
Sur le marché des pommes, l’offre des producteurs est modélisée par la fonction suivante :
\( f(x) = \left\{ \begin{array}{ll} 5- \dfrac{6}{x+3} \text { pour } 0 \leq x \leq 4 \\ 0,1(x-1)^2 +2 \text { pour } x > 4 \end{array} \right. \) où \(x\) est la quantité proposée, en centaine de kilogrammes et \(f(x)\) le prix en euro par cageot de 10kg.
Question 1
Calculer le prix au kg pour 300kg, puis pour 600kg.
\(f(3) = 5-1=4\).
4 est le prix par cageot de 10kg. On trouve donc 40 centimes par kg.
\(f(6) = 2,5 +2 = 4,5\).
4,5 est le prix par cageot de 10kg. On trouve donc 45 centimes par kg.
As-tu utilisé la bonne expression de \(f\) en fonction de l’ensemble de définition ? Attention ! Le résultat est demandé par kg et non par cageots de 10kg.
Question 2
Si un producteur vend 500kg, calculer le prix d'un cageot de 10kg. En déduire le chiffre d'affaire dégagé par la totalité de cette vente.
\(f(5) =1,6+2=3,6\).
Un cageot de 10kg vaut 3,6€ pour 500kg vendus.
\(3,6 \times50 = 180\).
Le chiffre d'affaire dégagé pour 500kg vendus est 180€.
Le calcul est évident ! Combien faut-il de cageots de 10kg pour obtenir 500kg ?
Question 3
Étudier le sens de variation de \(f\).
\( f'(x) = \left\{ \begin{array}{ll} \dfrac{6}{(x+3)^2}\text { pour } 0 \leq x \leq 4 \\ 0,2(x-1) \text { pour } x > 4 \end{array} \right. \)
Dans les deux cas, \(f'(x)\) est positive, donc \(f\) est croissante pour tout \(x\) sur \([0 ; +\infty[\).
Avez-vous dérivé les deux expressions ? Il faut raisonner séparément suivant les valeurs de \(x\).
Question 4
Étudier la continuité de cette offre.
\(f(4) = 5 - \dfrac{6}{7} \approx 4\) et
\( \displaystyle\lim_{x \to 4^+} f(x) = 2,9\)
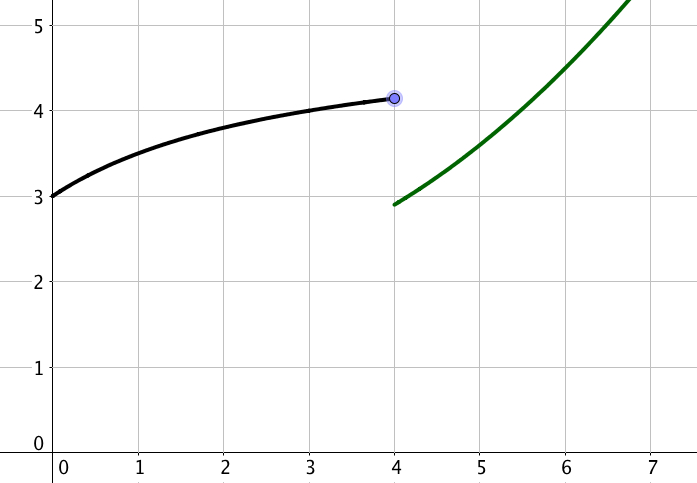
On ne peut donc pas tracer \(f\) sans lever le crayon, elle n'est pas continue sur \([0 ; +\infty[\).
Savez-vous ce qu’est une fonction continue ? Sinon, regardez la vidéo dans les prérequis.
Question 5
Est-elle concave ? Convexe ? Interpréter ce résultat.
Pour \(0 \leq x\leq 4, f''(x) = \dfrac{-12}{(x+3)^3}\)
\( f''(x)\) est négative, donc \(f\) est concave.
Pour \(x>4, f''(x) = 0,2\)
\(f''(x)\) est positive, donc \(f\) est convexe.
- Lorsque \(f\) est concave, le prix augmente faiblement en fonction du nombre de cageots vendus.
- Lorsque \(f\) est convexe, le prix augmente rapidement en fonction du nombre de cageots vendus.
Savez-vous ce qu’est une fonction concave ? Convexe ? Un doute ? Regardez la vidéo dans les prérequis.
