Une entreprise fabrique des clés USB avec un maximum de $10\:000$ unités par mois. Le coût de fabrication $C$ (en milliers d'euros) de $x$ milliers de clés produites s'exprime par :
$C(x)=0,05x^3 −1,05x^2 +8x+4.$
1) À l'aide de la calculatrice graphique, évaluer (ou conjecturer) la convexité de la fonction $C$. En déduire si la courbe possède un point d'inflexion.
2) Démontrer ces résultats.
3) Interpréter les résultats obtenus.
1) La fonction semble concave sur l'intervalle $[0 ; 7]$ et convexe sur l'intervalle $[7 ; 10]$.
La courbe semble posséder un point d'inflexion pour $x = 7$.

2) $C(x)=0,05x^3 −1,05x^2 +8x+4$
$C'(x)=0,15x^2 −2,1x+8$
$C ''(x) = 0,3x − 2,1$
Or $0,3x−2,1=0$ pour $x=7$.
On peut ainsi résumer les variations de $C'$ et la convexité de $C$ dans le tableau suivant :
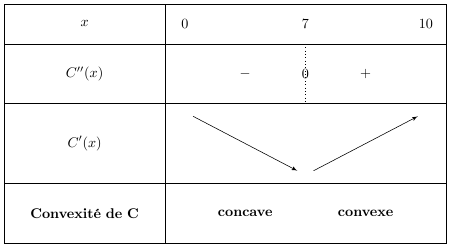
$C(7) = 25,7$.
Ainsi, le point de coordonnées $(7 ; 25,7)$ est un point d'inflexion de la courbe.
3) Pour $x\geq 7$, la fonction est convexe, la croissance du coût de fabrication $C$ s'accélère.
Pour $x\leq 7$, la fonction est concave, la croissance du coût de fabrication ralentit.
Ainsi, à partir de $7000$ clés produites, la croissance du coût de fabrication s'accélère.
