L'énoncé
Le coût, en euro, de \(x\) bouquets réalisés par un fleuriste est exprimé par la fonction suivante :
\(C(x) = 0,1x^2 - x +490\) pour \(x\) réel positif.
Soit \(CM(x)\) le coût moyen de \(x\) bouquets en euro par bouquet.
Question 1
Étudier le sens de variation de \(C\) sur \([0 ; +\infty]\).
\(C'(x) = 0,2x-1\)
\(0,2x -1 \geq 0 \Leftrightarrow x\geq5\)
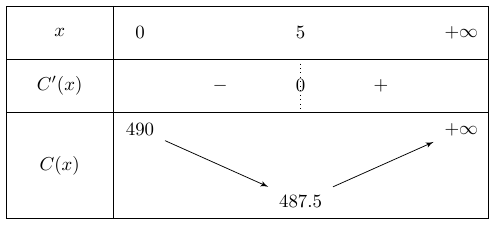
Avez-vous dérivé \(C\) ?
Saivez-vous dresser un tableau de variation ? Sinon, regardez la vidéo.
Question 2
Exprimer le coût moyen \(CM(x)\) par bouquet en fonction de \(x\).
\(CM(x) = \dfrac{C(x)}{x} = \dfrac{0,1x^2 -x+490}{x} \)
Sais-tu ce qu’est le coût moyen par rapport au coût total ?
Le coût total \(CM(x)\) est égal au coût total de production divisé par le nombre de produits fabriqués :
\(CM(x) = \dfrac{C(x)}{x}\)
Question 3
Étudier le sens de variation de \(CM\).
\(CM'(x) = \dfrac{(0,2x-1)x-(0,1x^2-x+490)}{x^2} = \dfrac{0,1x^2 -490}{x^2} \)
\(0,1x^2-490 \geq 0 \Leftrightarrow x^2 \geq 4900\)
Donc sur \([0; +\infty]\), \(x \geq 70\)
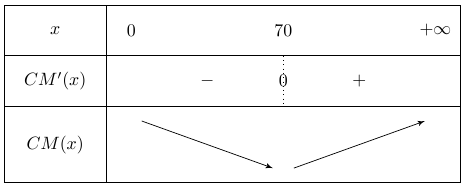
Avez-vous dérivé \(CM(x)\) ?
Avant de dresser le tableau de variations, il faut résoudre une équation du second degré pour trouver la valeur de \(x\) telle que \(CM(x) = 0\). Regardez l’ensemble de définition pour conclure.
Question 4
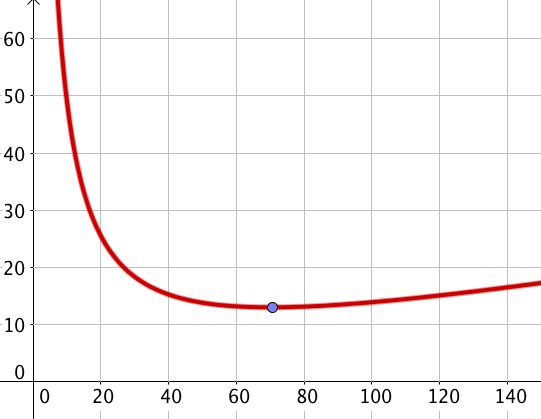
Quel est le nombre de bouquets à réaliser pour que le coût moyen par bouquet soit minimal ?
Daprès le tableau de variation précédent, \(CM\) admet un minimum pour \(x=70\). Il faut donc réaliser 70 bouquets pour que le coût moyen par bouquet soit minimum.
Il suffit de regarder le tableau de variation. La fonction \(CM\) admet-elle un minimum ?
