Espérance de la variable aléatoire

Espérance de la variable aléatoire

Définition

Soit $X$ une variable aléatoire et sa loi de probabilité :

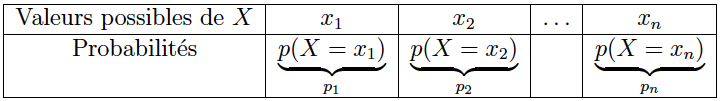
On appelle espérance de la variable aléatoire $X$, le nombre $E(X)$:

$E(X)=x_1 \times p_1+x_2 \times p_2+\ldots+x_n \times p_n$

$E(X)=\displaystyle\sum_{i=1}^{n}x_ip_i$

Exemple

Calculer l'espérance de $X$

$E(X)= -2 \times 0,2 + 3\times 0,3 + 5 \times 0,5 $

$E(X)=3$

Interprétation de l'espérance

L'espérance de $X$ représente la valeur moyenne de $X$ : c'est celle que l'on peut espérer obtenir en répétant un grand nombre de fois l'expérience.

Exemple

On lance une pièce truquée : la probabilité d'obtenir pile est de $0,6$.

• Si on obtient pile, on perd 1 euro.
• Si on obtient face , on gagne 2 euros.

Soit $X$ la variable aléatoire représentant le gain du joueur.  Déterminer interpréter son espérance.