L'énoncé
Une urne contient 5 boules indiscernables au toucher : 2 rouges et 3 bleues.
On tire au hasard une boule dans l’urne, et on note sa couleur. Puis on la remet dans l’urne, et on répète une fois cette expérience.
On notera $R$ : "la boule est rouge" et $B$ : la boule est bleue.
Tu as obtenu le score de
Question 1
La probabilité d'obtenir deux fois une boule bleue (résultat noté B-B) est :
\(\dfrac{3}{5}\)
\(\dfrac{9}{25}\)
\(\dfrac{6}{5}\)
\(0,6\)
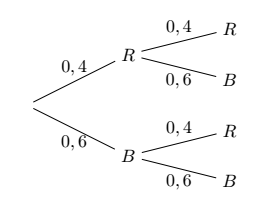
Suivre le chemin B-B
Lorsqu’on a un arbre pondéré, la probabilité d’un chemin est égale au produit des probabilités inscrites sur les branches de ce chemin.
Lorsqu’on a un arbre pondéré, la probabilité d’un chemin est égale au produit des probabilités inscrites sur les branches de ce chemin.
On repère le chemin B-B (en bas).
La probabilité de ce chemin est alors \(P= \frac{3}{5} \times \frac{3}{5} = \frac{9}{25}=0,36\).
Proposition 2 vraie.
Question 2
On note \(X\) la variable aléatoire égale au nombre de fois où l'on a tiré une boule rouge.
Cocher la bonne réponse.
Les valeurs possibles de \(X\) sont \(1\) et \(2\).
Les valeurs possibles de \(X\) sont \(0;1\) et \(2\).
\(p(X=2)= \dfrac{4}{25}\)
\(p(X=2)= \dfrac{8}{25}\)
On tire deux fois une boule dans l’urne : au maximum, on obtient deux fois une boule rouge.
L’évènement \(X=2\) correspond au tirage R-R : utilise l’arbre et la règle révisée à la question 1 pour trouver la probabilité de ce chemin !
Les valeurs de \(X\) sont 0, 1 ou 2.
Proposition 2 juste.
Toujours grâce à l’arbre obtenu, et en prenant le chemin R-R, on voit que :
\(p(X=2)=p(R-R)=\frac{2}{5} \times \frac{2}{5} = \frac{4}{25}\)
Proposition 3 juste.
Question 3
La loi de probabilité de \(X\) est :
| \(X\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{2}{5}\) | \(\frac{3}{5}\) |
| \(X\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{6}{25}\) | \(\frac{4}{25}\) |
| \(X\) | \(0\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{9}{25}\) | \(\frac{6}{25}\) | \(\frac{4}{25}\) |
| \(X\) | \(0\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{9}{25}\) | \(\frac{12}{25}\) | \(\frac{4}{25}\) |
Pour donner une loi de probabilité, il faut faire un tableau avec toutes les valeurs possibles pour \(X\) et leurs probabilités.
Utilise les résultats des questions précédentes : quelles cases peux-tu facilement remplir ?
Pour trouver \(p(X=1)\), tu peux utiliser que la somme des probabilités doit être égale à 1... ou la calculer par lecture de l’arbre.
On a déjà :
\(p(X=0)=\) probabilité d’avoir 0 boule rouge, soit 2 boules bleues = \(\dfrac{9}{25}\) (question 1)
\(p(X=2)= \) probabilité d’avoir 2 boules rouges = \(\dfrac{4}{25}\) (question 2)
Donc la loi de probabilité est :
| \(X\) | \(0\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{9}{25}\) | \(?\) | \(\frac{4}{25}\) |
Pour \(p(X=1)\) : on utilise que \(\frac{9}{25} +p (X=1) + \frac{4}{25} = 1\)
Donc \(p(X=1) = 1- \frac{13}{25} = \frac{12}{25} \)
Proposition 4 vraie.
Question 4
On a :
\(p(X\leq1) = \dfrac{21}{25}\)
\(p(X\leq1) =\dfrac{108}{25}\)
La probabilité d’avoir au plus une boule rouge est \(\dfrac{21}{25}\).
La probabilité d’avoir au plus une boule rouge est \(\dfrac{4}{25}\).
\(X\leq1\) correspond à \( X=0\) ou \( X=1\).
\(p(X\leq1) = p(X=0) + p(X=1)\)
Avoir au plus une boule rouge signifie qu’au maximum, le nombre de boule rouge est 1 : à traduire sur \(X\).
\(p(X\leq1) = p(X=0) + p(X=1) = \frac{9}{25}+ \frac{12}{25}= \frac{21}{25} \)
Proposition 1 vraie.
Avoir au plus une boule rouge signifie qu’au maximum, le nombre de boule rouge est 1 :
il peut donc être égal à 0 ou à 1 : c’est \(\frac{21}{25}\)
Proposition 3 vraie.
Question 5
Cocher la ou les bonne(s) réponse(s) :
| \(X\) | \(0\) | \(1\) | \(2\) |
| \(p(X=x_i)=p_i\) | \(\frac{9}{25}\) | \(\frac{12}{25}\) | \(\frac{4}{25}\) |
L'espérance de \(X\) est :
\(0,6\)
\(0,8\)
\(\dfrac{4}{5}\)
\(\dfrac{13}{25}\)
\( E(X) = 0 \times \frac{9}{25} + 1 \times \frac{12}{25} +...\)
\( E(X) = 0 \times \frac{9}{25} + 1 \times \frac{12}{25} + 2 \times \frac{4}{25}\)
\( E(X) = \frac{20}{25} = \frac{4}{5} =0,8\)
Propositions 2 et 3 vraies.
