Fiche de cours
Limite infinie d'une fonction en un réel a
Définitions
$\bullet$ Soit $a$ un réel. Une fonction $f$ tend vers $+\infty$ quand $x$ tend vers $a$ si, pour tout réel $A$, il existe un intervalle centré en $a$ tel que pour tous les $x$ appartenant à cet intervalle, on a : $f(x)>A$.
On note $\displaystyle \lim_{x\to a} f(x)=+\infty$.
$\bullet$ Si $\displaystyle \lim_{x\to a} f(x) = \pm \infty$ alors la droite d'équation $x=a$ est une asymptote verticale à la courbe représentative de $f$.
Ces définitions sont de même nature si $f$ tend vers $-\infty$ ou si on étudie les limites à gauche ou à droite de la fonction.
Illustrations graphiques
On va ici prendre en exemple le point $x=5$ mais les remarques et illustrations graphiques seront valables pour n'importe quel point $x=a$ avec $a\in \mathbb{R}$.
1)
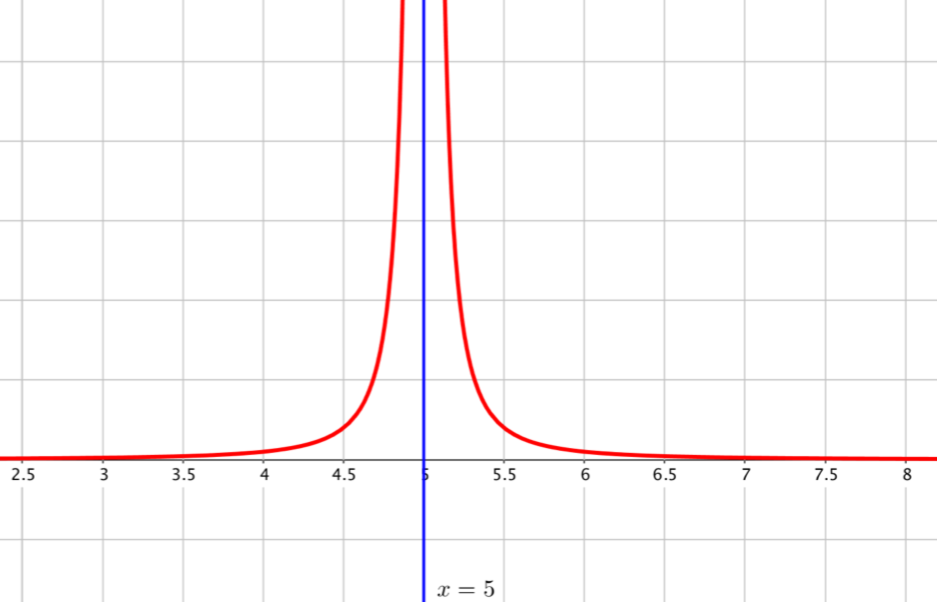
Sur la figure $1$, le nombre $x=5$ est une "valeur interdite" de la fonction représentée en rouge.
On constate que lorsque $x$ se rapproche de $5$ (par la droite ou par la gauche), $f(x)$ est de plus en plus grand.
On dit alors que $f$ tend vers $+\infty$ quand $x$ tend vers $5$ et on note $\dis
