1) $f(x) = 3 \cos x$

$f$ est du type $k \times \cos$, donc $f'$ est du type $-k \times \sin$

Ici on a : $f'(x) = -3 \times \sin x$

$f'(x) > 0 \iff -3 \sin x > 0 \iff \sin x < 0$

D'après le cercle trigonométrique, $f'(x) > 0$ si $x$ appartient à l'intervalle $[- \pi ; 0 [$

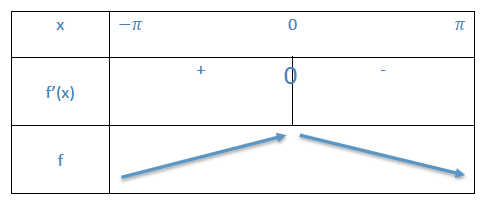
2) $g(x) = 2 \sin x + 1$

On a $f$ du type $k \times \sin + 1$, $g'$ est du type $k \times \cos$ d'où $g'(x) = 2 \cos x$

De la même façon que précédemment, on résout $g'(x) > 0$ et on obtient $\cos x > 0$.

$g'(x) > 0$ si $x$ appartient à l'intervalle $\left \rbrack -\dfrac{\pi}{2} ; \dfrac{\pi}{2} \right \lbrack$

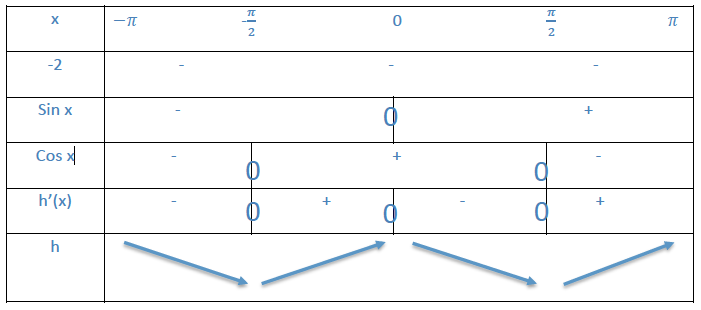
3) $h(x) = \cos^2 x$

On a $h = u^n$

$U(x) = \cos x$ et $n =2$

$h' = n \times u' u^{n-1} \iff h'(x) = -2 \sin x \cos x$

On résout $h'(x) > 0$

$\cos x > 0$ si $x$ appartient à $\left \rbrack - \dfrac{\pi}{2} ; \dfrac{\pi}{2} \right \lbrack$

$\sin x > 0$ si $x$ appartient à $]0;\pi[$