Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Inéquations trigonométriques
Résolution graphique
On souhaite résoudre sur $[0,2\pi]$ l'inéquation suivante : $\cos(x)\leqslant \dfrac12$.
On sait que $\cos\left(\dfrac{\pi}{3}\right)=\dfrac12$ et $\cos\left(-\dfrac{\pi}{3}\right)=\dfrac12$.
Ici, on veut résoudre l'équation sur $[0,2\pi]$ donc on écrit
$-\dfrac{\pi}{3}=-\dfrac{\pi}{3}+2\pi= \dfrac{5\pi}{3}$ $[2\pi]$.
On constate alors que tous les $x$ compris dans la zone surlignée en rouge ont un cosinus inférieur à $\dfrac12$.
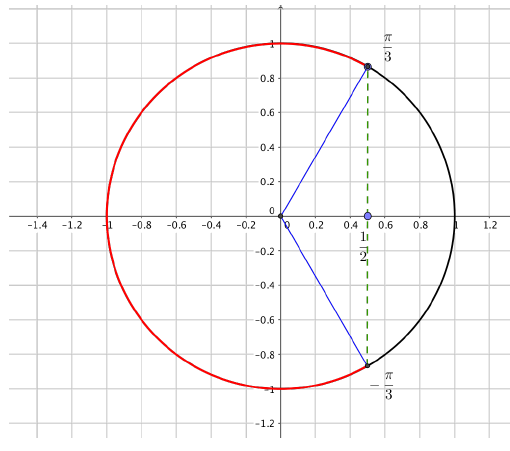
Ensemble de solutions
On peut alors simplement donner l'ensemble de solutions de l'inéquation de départ :
$ \mathcal{S}= \left[ \dfrac{\pi}{3};\dfrac{5\pi}{3} \right]$
