L'énoncé
Partie A
Soit la fonction \(f\) définie sur \(]0;+\infty[\) par : \(f(x) = ax+(bx + c)\ln(x)\) avec \(a\), \(b\) et \(c\) des réels.
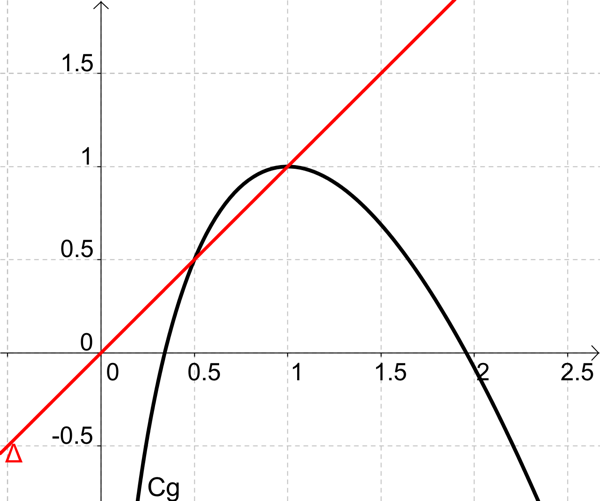
La courbe \((C)\) représentative de \(f\) est donnée ci-dessous.
Question 1
En utilisant le graphique et en sachant que \(f(2)=2-3\ln(2)\), justifier que : \(a=c=1\) et \(b=-2\).
\(f(2) = 2-3\ln(2) \Rightarrow 2a+(2b+c)\ln(2) = 2-3\ln(2)\)
Par ailleurs la dérivée s'annule en $1$, donc :
\(f'(x) = a+b\ln(x)+\dfrac{bx+c}{x} \Rightarrow a+0+\dfrac{b+c}{1} = 0\)
\( \Leftrightarrow a+b+c=0\) et \(f(1) = 1\) donc : \(f(1) = a+0 = a = 1\).
On a donc:
\(2+(2b+c)\ln(2) = 2-3\ln(2) \Rightarrow 2b+c=-3\) avec \(1+b+c =0\)
On tire par la résolution d'un système à deux inconnues \(c=1\) et \(b=-2\).
La valeur de \(f(2)\) donne une équation avec les réels inconnus.
On voit aussi graphiquement la valeur de \(f(1)\).
Observez la courbe. La tangente est horizontale en un point donné.
Que vaut la dérivée en ce point pour que la tangente soit horizontale ?
Avec ces trois équations, vous pouvez trouver \(a\), \(b\) et \(c\).
Question 2
Partie B
On considère alors la fonction \(g\) définie sur \(]0;+\infty[\) par : \(g(x) = x+(1-2x)\ln(x)\)
Déterminer la limite de \(g\) au voisinage de $0$ par valeur supérieure.
Au voisinage de $0$, \(\ln(x)\) tend vers \(-\infty\), donc \(g\) tend vers \(-\infty\).
Pour la limite, il n’y a pas de forme indéterminée.
Question 3
Déterminer la limite de \(g\) au voisinage de \(+\infty\).
Mettons \(x\) en facteur :
Pour tout \(x\in ]0;+\infty[\) , \(g(x) = x \left[ 1+\left(\dfrac{1}{x}-2\right)\ln(x)\right]\)
Il n'y a pas de forme indéterminée. Par produit de limites, on obtient :
\( \lim _{x\to +\infty}g(x) = -\infty\)
Pour la limite en \(+\infty\), factoriser l’expression par \(x\). L’indétermination sera levée.
Question 4
Déterminer la fonction dérivée de \(g\).
Pour tout \(x\in ]0;+\infty[\)
\(g'(x) = 1-2\ln(x)+\dfrac{1-2x}{x}\)
\(g'(x) = \dfrac{x-2x\ln(x)+1-2x}{x}\)
\(g'(x) = \dfrac{1-x-2x\ln(x)}{x} \)
Retrouvez la dérivée de \(\ln(x)\).
Rappelez-vous la dérivée d’un produit : \((uv)’ = u’v + uv’\)
Question 5
Etudier, pour \(x \in ]0;+\infty[\), le signe de \(-2\ln(x)\) et celui de \(\dfrac{1-x}{x}\).
En déduire le signe de \(g'(x)\).
\(-2\ln(x)\) change de signe en $1$, de même que \(\dfrac{1-x}{x}\) puisque \(x\) est positif.
\(-2\ln(x)\) est donc positif avant $1$ et négatif après $1$.
Il en est de même pour \(\dfrac{1-x}{x}\) qui est positif pour \(0 < x \leq 1\) et négatif sur \([1,+\infty[\).
La dérivée est constituée de deux termes qui changent de signe pour la même valeur et de même signe de part et d'autre de cette valeur : avant $1$ elle est positive, après $1$ elle est négative.
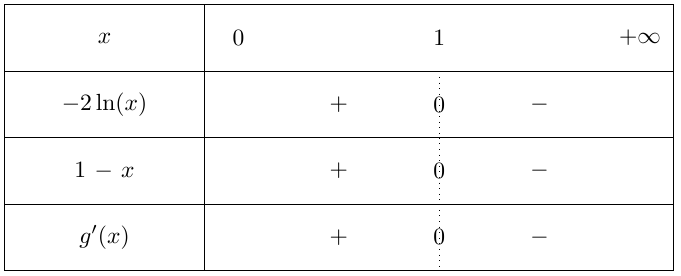
Ces deux termes changent de signe pour la même valeur. Il en est de même pour leur somme.
Faites un tableau de valeurs pour vous aider.
Question 6
Dresser le tableau complet des variations de \(g\).
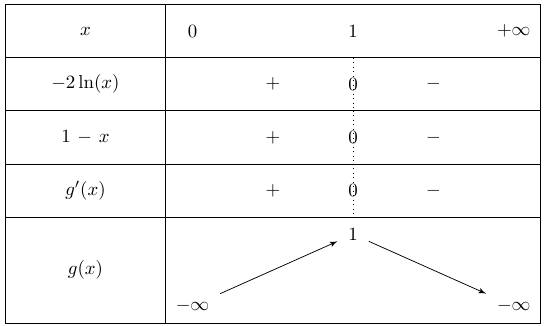
Connaissant le signe de \(g’\), on en déduit les variations de \(g\).
N’oubliez pas les limites aux bornes de l’intervalle.
Question 7
Soit la droite \(\Delta\) d'équation \(y=x\).
Résoudre dans \(\mathbb{R}^*\) l'équation : \((1-2x)\ln(x) =0\)
\((1-2x)\ln(x) = 0\)
\( \Leftrightarrow \left\{ \begin{array}{left} 1-2x = 0 \\ \ln(x) =0 \end{array}\right.\)
\( \Leftrightarrow x = \dfrac{1}{2}\) ou \(x=1\).
Ces deux solutions sont bien des réels strictement positifs (et appartiennent donc à \(D_g\)).
C’est une équation produit.
Ce produit est nul si et seulement si l’un au moins des facteurs est nul.
Question 8
Etudier la position de la courbe représentative de \(g\) par rapport à \(\Delta\).
Chercher la position relative des deux courbes c'est étudier le signe de la différence : \(g(x) - x = (1-2x)\ln(x)\)
D'après la question précédente, on connaît les valeurs pour lesquelles \(g(x)-x\) s'annule. On en déduit le tableau de signe :
Un rapide tableau de signe nous prouve que \(g(x)-x\) est positif sur \(\left[\dfrac{1}{2};1\right]\) : Sur cet intervalle, \(C\) est au-dessus de \(\Delta\) ; sinon \(C\) est en dessous de \(\Delta\).
Il apparait que \(g(x) – x =0\) revient à résoudre une équation fraichement résolue.
Etudiez le signe de \(g(x) – x\).
Si \(g(x) - x \geq 0\) on peut en déduire que la courbe \(C\) est au dessus de \(\Delta\)