$f$ est une fonction définie sur $\mathbb{R}$ par $f(x) = \dfrac{x^3}{3} - x^2 - 8x$
1. Calculer $f’(x)$ pour tout réel $x$.
2. Etudier le signe de $f’(x)$ et dresser le tableau de variation de la fonction $f$.
3. a) Déterminer une équation de la tangente $T$ à $C_f$ au point d’abscisse $0$.
b) Etudier la position de $C_f$ par rapport à $T$.
La courbe $C_f$ admet-elle une(des) tangente(s) parallèle(s) à la droite d’équation $y = -5 x + 1$ ? En quels points ?
1. $f'(x) = x^2 - 2x - 8$
2. $f'$ est une fonction polynôme du second degré, donc on trouve les racines du polynôme avec le discriminent $\Delta$.
Les racines sont $-2$ et $4$ donc on obtient le tableau de variation suivant :
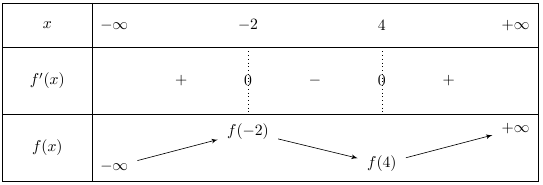
avec $f(-2) = -9,33$ et $f(4) = -26,66$
3. a) $y = -8x$.
b) Il faut étudier le signe de l’écart $f(x) – (-8x)$ et pas $f(x) - T$ qui ne veut rien dire.
Or $f(x) – (-8x) = \dfrac{x^3}{3} - x^2 $
$f(x)+8x = x^2(\dfrac{x}{3} - 1) = \dfrac{x^2(x-3)}{3}$ donc on obtient facilement la position de la courbe par rapport à la tangente $T$:

Les tangentes à $C_f$ aux points d’abscisse $x$ sont parallèles à $D$ si elles ont le même coefficient directeur que $D$ donc si $f'(x) = -5$.
Il faut résoudre l’équation $f'(x) = -5$
Soit $x^2 - 2x – 8 = -5$ ou $x^2 - 2x – 3 = 0$.
Les solutions sont $x=-1$ et $x = 3$ qui sont les abscisses des points cherchés.
$A(-1 ; f(-1))$ et $B(3 ; f(3))$ soit $A\left(-1 ; \dfrac{20}{3}\right)$ et $B(3 ; -24)$.
