1) Soit $U$ et $V$ les fonctions définies respectivement sur $\mathbb{R}$ et $\mathbb{R}-\{0\}$ par :
$U(x) =x^2$
$V(x) =\dfrac{1}{x^3}$
Tracer les courbes représentatives $\mathcal{C_u}$ et $\mathcal{C_v}$, des fonctions respectives $U$ et $V$ dans un repère $\mathcal{(O, \vec{i}, \vec{j})}$.
2) Déterminer les points d’intersection des courbes $\mathcal{C_u}$ et $\mathcal{C_v}$ par lecture graphique.
3) Tracer les tableaux de variations de ces 2 fonctions.
1) Soit $U$ et $V$ les fonctions définies respectivement sur $\mathbb{R}$ et $\mathbb{R}-\{0\}$ par :
$U(x) =x^2$
$V(x) =\dfrac{1}{x^3}$
Tracer les courbes représentatives $\mathcal{C_u}$ et $\mathcal{C_v}$ ,des fonctions respectives U et V dans un repère $\mathcal{(O, \vec{i}, \vec{j})}$.
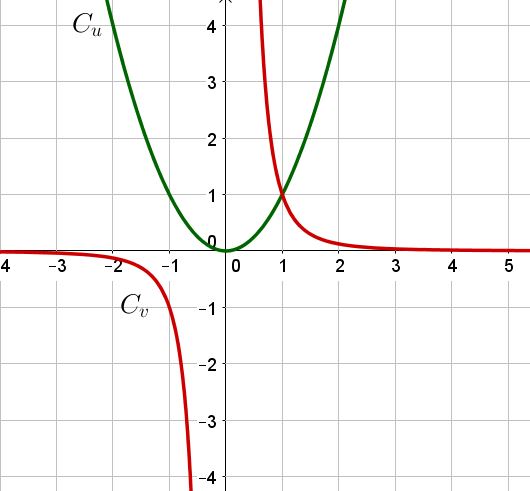
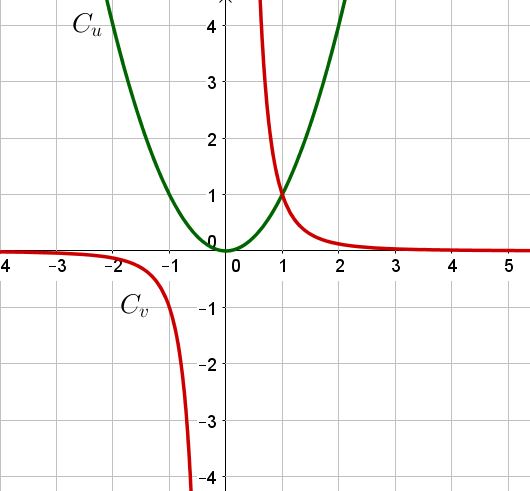
2) Les courbes se coupent au point de coordonnées $(1 ;1)$ On vérifie que $U(1) = V(1) = 1$.
3)

