L'énoncé
On considère la fonction $f(x) = \ln(1+x^2)$
Question 1
Étudier le domaine de définition et les variations de $f$.
Le domaine est $\mathbb{R}$ car $1+ x^2 > 1$ et $f(x) =\ln (1+x^2)$ existe pour tout réel.
On calcule la dérivée :
Pour tout réel $x$,
$f'(x) = \dfrac{2x}{1+x^2}$
$f'(x) = 0 \iff \dfrac{2x}{1+x^2} = 0 \iff x = 0$
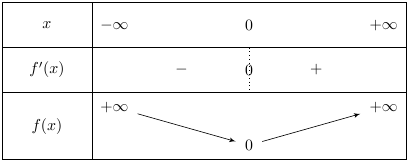
On en déduit le tableau de variations suivant :
Question 2
Etudier la convexité et concavité et les points d'inflexion de la fonction.
Pour tout réel $x$,
$f''(x) = \dfrac{2(1+ x^2) - 2x \cdot 2x}{(1+x^2)^2}$
$f''(x) = \dfrac{2+2x^2 - 4x^2}{(1+x^2)^2}$
$f''(x) = \dfrac{2-2x^2}{(1+x^2)^2}$
On analyse $f'' (x)$ :
$f''(x) = 0 \iff \dfrac{2-2x^2}{(1+x^2)^2} = 0 \iff 2 - 2x^2 = 0 \iff x = \pm 1$
Il y a donc deux points d'inflexion obtenus lorsque $x=1$ et $x=-1$.
On en déduit le signe de $f''(x)$ :
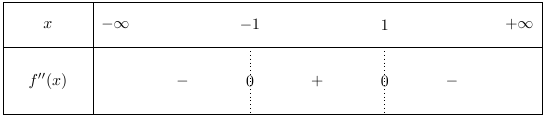
Finalement on a :
$f$ est convexe sur $]-1 \ ; \ 1 [$
$f$ est concave sur $]- \infty \ ; \ -1[ $ et $ ]1 \ ; \ + \infty [$
Points d'inflexion : $(-1 , \ln2)$ et $(1, \ln2)$
Question 3
Quelle est l'équation de la tangente à la courbe en $x=0$ ?
La fonction admet une dérivée nulle en $0$
D'autre part, $f(0)=\ln(0+1)=0$
Ainsi l'équation de la tangente est $y=0$
Il s'agit de l'axe des abscisses.
Question 4
A l'aide de votre calculatrice, tracer la courbe représentative de $f(x) = \ln (1+x^2)$ en utilisant les informations obtenues.
La fonction est symétrique par rapport à l'axe des ordonnées car elle elle paire.
(On peut vérifier que $f(-x)=f(x)$ pour tout réel)
Les points d'inflexion sont en bleu.
.png?1587559297184)
