L'énoncé
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=x^2e^{1-x}\)
On désigne par \(C\) sa courbe représentative dans un repère orthonormal \((O ; \vec{i} ; \vec{j})\).
Question 1
Déterminer les limites de \(f\) au voisinage de \(-\infty\) et de \(+\infty\) ; quelles conséquences graphique pour \(C\) peut-on en tirer ?
Au voisinage de \(-\infty\), \(f(x)=x^2e^{1-x}\) tend vers \(+\infty\) car les deux termes tendent vers \(+\infty\).
$\displaystyle\lim_{x \to -\infty}f(x)=+\infty$.
On ne peut rien conclure graphiquement.
On remarque que : \(f(x)=x^2e^{1-x} =x^2\times e \times e^{-x}\)
D'après le théorème des croissances comparées, on sait que $\displaystyle\lim_{x \to +\infty}\dfrac{e^x}{x^2}=+\infty$
Donc en passant au quotient : $\displaystyle\lim_{x \to +\infty}\dfrac{x^2}{e^x}=0$ ou encore $\displaystyle\lim_{x \to +\infty}x^2\times e^{-x}=0$
Conclusion : $\displaystyle\lim_{x \to +\infty}f(x)=0$
On a alors une asymptote horizontale \(y = 0\).
Il y a une forme indéterminée au voisinage de \(+\infty\). Utilisez le théorème de croissances comparées. Un oubli ? Revoyez la vidéo de rappel sur ce théorème via les pré-requis.
Une des deux limites conduit à la présence d’une asymptote. Laquelle ?
Question 2
Justifier que \(f\) est dérivable sur \(\mathbb{R}\). Déterminer sa fonction dérivée \(f \).
\(f\) est le produit de fonctions dérivables sur \(\mathbb{R}\) et est donc dérivable sur \(\mathbb{R}\).
On a :
\(f'(x)=2xe^{1-x}-x^2e^{1-x} \)
\(f'(x)= x(2-x)e^{1-x}\)
La dérivabilité ne pose aucun souci. « Le produit de deux fonctions dérivable est… »
Dérivez la fonction qui est sous forme d’un produit.
Un oubli ? \((uv)’ = u’v+uv’\)
Question 3
Dresser le tableau de variations de \(f\) et tracer la courbe \(C\).
Comme l'exponentielle est positive, \(f\) est du signe de \(x( 2 - x )\).
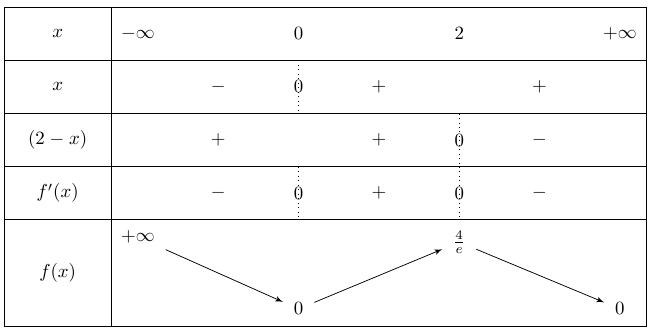
Montrez que \(f’(x)\) est du signe de \(x(2-x)\).
Faites un tableau de signes pour la dérivée et dressez le tableau de variations de \(f\).
Pensez à reporter les limites. Calculez \(f(0)\) et \(f(2)\).
Question 4
Soit \(n\) un entier naturel non nul. On considère l'intégrale \(I_n\) définie par \(I_n=\displaystyle\int_0^1 x^ne^{1-x}\,dx\)
On admet que : \(I_{n+1} = -1 +(n+1)I_n \) et on donne \(I_{1}=e-2 \)
Calculer \(I_2\).
Par application de la formule de récurrence, on trouve :
\(I_2 = -1 +2 I_1 = -1 + 2(e-2) = 2e-5\)
Avez-vous pensé à utiliser la relation de récurrence donnée dans l'énoncé ?
Question 5
Donner une interprétation graphique du nombre \(I_2\). On la fera apparaître sur le graphique construit lors de la question 3.
Il s'agit de l'aire du domaine délimité par \(C\), l'axe horizontal et les droites d'équation \(x = 0\) et \(x = 1\).
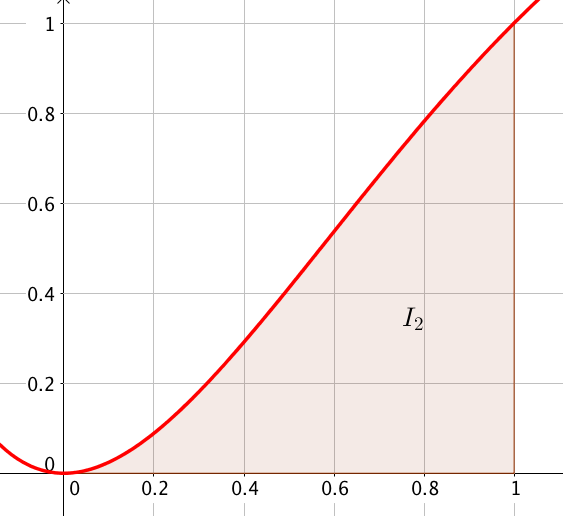
C’est une question de cours.
Il s’agit d’une aire délimitée par des droites et des portions de courbes.
Question 6
Démontrer que pour tout nombre réel \(x\) de \(\left[0 ; 1\right]\) et pour tout entier naturel \(n\) non nul, on a l'inégalité suivante :
\(x^n \leq x^ne^{1-x} \leq x^ne\)
\(0\leq x\leq 1\)
\( \Leftrightarrow -1\leq -x\leq 0\)
\( \Leftrightarrow 0\leq 1-x\leq 1\)
\( \Leftrightarrow e^0\leq e^{1-x}\leq e^1\)
Or, \(x^n>0\) donc :
\(0\leq x\leq 1\Leftrightarrow x^n\leq x^ne^{1-x}\leq x^ne \)
Partez de l’encadrement de \(x\) proposé.
\(0\leq x \leq 1\) bien sur.
Encadrez \(-x\) puis \(1-x\).
Faites intervenir l’exponentielle dans cet encadrement. (Fonction croissante)
Multipliez chaque membre par \(x^n\) (Songez au signe de ce terme). Concluez.
Question 7
En déduire un encadrement de \(I_n\) puis la limite de \(I_n\) quand \(n\) tend vers \(+\infty\).
On intègre l'inégalité précédente entre $0$ et $1$ :
\( \displaystyle \int_0^1 x^n \, dx \leq \displaystyle \int_0^1 x^ne^{1-x} \, dx \leq \displaystyle \int_0^1 x^ne \, dx\)
\( \Leftrightarrow \left[\dfrac{1}{n+1}x^{n+1}\right]_0^1 \leq I_n \leq e\left[\dfrac{1}{n+1}x^{n+1}\right]_0^1\)
\( \Leftrightarrow \dfrac{1}{n+1}\leq I_n \leq \dfrac{e}{n+1} \)
Donc \(I_n\) tend vers $0$ grâce à nos amis les gendarmes
Le théorème... vous aviez compris...
$\displaystyle\lim_{n \to +\infty}I_n=0$
Intégrez l’inégalité trouvée à la question 6 entre $0$ et $1$.
En effet, si \(f(x) \leq g(x) \leq h(x)\) sur \(\left[0;1\right]\) alors \(\displaystyle \int_0^1 f(x) \, dx \leq \displaystyle \int_0^1 g(x) \, dx \leq \displaystyle \int_0^1 h(x) \, dx\).
Vous obtenez un encadrement de \(I_n\) en fonction de \(n\).
Etudiez la limite des membres de gauche et de droite.
Utilisez un théorème célèbre pour conclure.
Celui des gendarmes bien sur. Un oubli ? Voir le rappel dans les pré-requis.
