L'énoncé
Soit la fonction définie sur l'intervalle \(I = \left]4 ; +\infty \right[\) par :
\(f(x)=-2x+5+3\ln\left(\dfrac{x+1}{x-4}\right)\) et \((C_f)\) sa courbe représentative dans le repère orthonormal \((O ; \vec{i}, \vec{j} )\).
Question 1
Étude de \(f\)
Étudier les limites de la fonction \(f\) aux bornes de \(I\).
Lorsque \(x\) tend vers 4 par valeur supérieure, \(\dfrac{x+1}{x-4}\) tend vers \(+\infty\) ainsi que \(\ln\left(\dfrac{x+1}{x-4}\right)\) donc :
$\displaystyle\lim_{x\to 4^+}f(x)=+\infty$
Lorsque x tend vers \(+\infty\), \(\dfrac{x+1}{x-4}\) tend vers 1 et \(\ln\left(\dfrac{x+1}{x-4}\right)\) tend vers 0,
On sait aussi que : \(-2x+5\) tend vers \(-\infty\) donc
$\displaystyle\lim_{x\to +\infty}f(x)=-\infty$
Dans ce cas, $x-4$ tend vers $0$ en restant positif.
Il n’y a pas de forme indéterminée lorsque \(x\) tend vers 4.
Question 2
Montrer que sur \(I\), \(f '(x)\) est strictement négative et donnez les variations de \(f\).
\(f'(x)=-2+3\left(\ln\left(\dfrac{x+1}{x-4}\right)\right)'\).
\(f'(x) =-2+3\left(\ln(x+1)-\ln(x-4)\right)'\)
\(f'(x) =-2+3\left(\dfrac{1}{x+1}-\dfrac{1}{x-4}\right)\)
\(f'(x) =\dfrac{-2(x+1)(x-4)-15}{(x+1)(x-4)}\)
Lorsque \(x > 4\), \(x+1\) est positif.
\(x-4\) est aussi positif donc le numérateur est négatif et le dénominateur est positif.
Conclusion, \(f'\) est négative sur \(I\) et \(f\) est donc décroissante sur son ensemble de définition.
Dérivez \(f\) sur son ensemble de définition.
Un oubli sur la dérivée de \(\ln(u(x))\) ? Revoyez bien les pré-requis sur le logarithme népérien.
Question 3
Une primitive de la fonction \(x \rightarrow \ln (x)\) est : \(x\ln(x)-x\).
Montrer que sur \(I\), la fonction \(g : x \mapsto \ln (x + 1)\) admet pour primitive la fonction :
\(G(x)= (x + 1) \ln (x + 1) - x\)
On dérive \(G\) :
\(G'(x)=1\times \ln(x+1)+(x+1)\dfrac{1}{x+1}-1=\ln(x+1)\)
Il suffit de vérifier que \(F’(x) =f(x)\). c’est la définition.
Appliquez ceci aux fonctions proposées.
Question 4
Montrer que sur \(I\), la fonction \(h : x \mapsto \ln (x - 4)\) admet pour primitive la fonction
\(H (x)= (x - 4) \ln(x - 4) - x\)
On dérive \(H \):
\(H'(x)=1\times \ln(x-4)+(x-4)\dfrac{1}{x-4}-1=\ln(x-4)\)
Il suffit de vérifier que \(F’(x) =f(x)\). c’est la définition.
Appliquez ceci aux fonctions proposées.
Question 5
Déduire des questions précédentes le calcul de l'aire \(A\) du domaine plan délimité par la courbe \((C_f)\), la droite \((D)\) d'équation \(y = - 2x + 5\) et les droites d'équations respectives \(x = 5\) et \(x = 6\).
On donnera la valeur exacte de \(A\) puis une valeur approchée à \(10^{-2}\) près.
On cherche \(A=\displaystyle \int_5^6 f (x)-(-2x + 5)\,dx\)
\(A=3\displaystyle \int_5^6 \ln(x + 1)- \ln(4 - x)\,dx\)
\(A=3\left[G(6)-G(5)\right]- 3\left[H(6) - H(5)\right]\)
Or, \(G(6)-G(5) = 7 \ln(7) - 6 - 6 \ln (6) + 5\)
\(G(6)-G(5) = 7 \ln(7) -6 \ln (6) -1\)
De plus, \(H(6)- H(5) = 2 \ln (2) - 6 -1\ln(1)+ 5\)
\(H(6)-H(5) = 2 \ln (2) -1 \)
Ainsi :
\(A = 3\left( 7 \ln(7) - 6 \ln(6) - 2\ln (2) \right) \approx 4,45 \)u.a
Voici une représentation graphique de $f$ et de la droite $D$.
La valeur de $A$ est représenté (au signe près) par l'aire de la partie colorée.
Le nombre $A$ est positif car la courbe \(C_f\) est au dessus de la droite lorsque $x$ est compris entre $5$ et $6$.
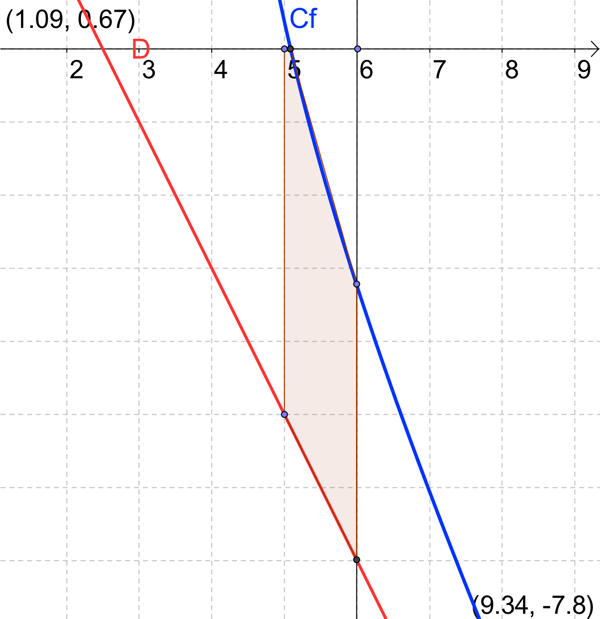
Attention, faites une figure pour bien visualiser l’aire demandée.
D’après votre cours, \(A=\displaystyle \int_5^6 f (x)\,dx-\displaystyle \int_5^6 -2x+5\,dx\).
Utilisez les primitives trouvées précédemment et conclure.
