L'énoncé
Cet exercice est un QCM. Coche la ou les bonne(s) réponse(s).
Tu as obtenu le score de
Question 1
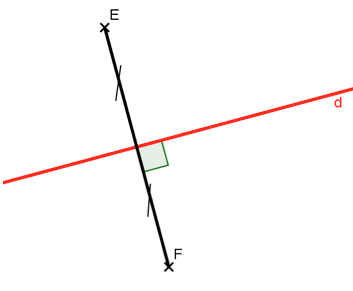
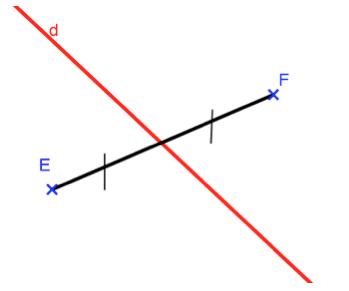
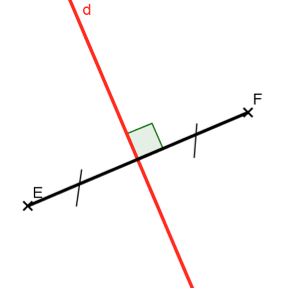
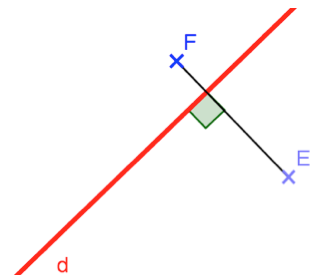
Pour quelle(s) situation(s) présentées ci-dessous, les points \(E\) et \(F\) semblent-ils symétriques par rapport à la droite \(d\) ?
\(E \) et \(F\) sont symétriques par rapport à \(d\) lorsque $d$ est la médiatrice de \([EF]\).
Observe bien les codages.
On doit avoir : \((d)\perp (EF)\) et \(d\) passe par le milieu de \([EF]\).
Pour pouvoir affirmer que \(E\) et \(F\) sont symétriques par rapport à \(d\) on doit lire les deux codages : celui de l’angle droit et celui des deux longueurs égales.
Question 2
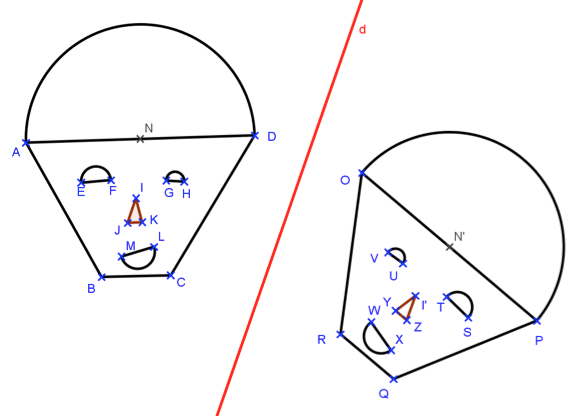
Dans la figure ci-contre, on donne : \(N\) est le milieu de \([AD\)],
\(AD=6cm\), \(AB=5cm\), \(BC=2cm\), \(CD=5,5cm\), \(EF=1cm\), \(GH=0,5cm\) et \(ML=1,5cm\).
\(\widehat{ADC}=43°, \widehat{BCD}=110°, \widehat{DAB}=57\)° et \(\widehat{ABC}=102°\)
Quelle est la longueur de \([PN']\) ?
6 cm
4 cm
3 cm
\(BC\)
Détermine le symétrique de \([PN’]\) par rapport à \(d\).
Que représente \(N\) pour \([AD]\) ?
Que représente \(N’\) pour \([OP]\) ?
\(N\) est le milieu de \([AD]\). \(N'\) est le symétrique de \(N\) et \([OP]\) celui de \([AD]\) par rapport à \(d\).
Or la symétrie conserve les longueurs et les milieux.
Donc \(N'\) est le milieu de \([OP]\).
Question 3
Dans la figure ci-contre, on donne : \(N\) est le milieu de \([AD\)],
\(AD=6cm\), \(AB=5cm\), \(BC=2cm\), \(CD=5,5cm\), \(EF=1cm\), \(GH=0,5cm\) et \(ML=1,5cm\).
\(\widehat{ADC}=43°, \widehat{BCD}=110°, \widehat{DAB}=57\)° et \(\widehat{ABC}=102°\)
Quelle est la longueur de \([QP]\) ?
6 cm
5,5 cm
5 cm
2 cm
\([QP] \) est le symétrique de… ?
La symétrie conserve les longueurs.
Quelle est la longueur du symétrique de \([QP]\) ?
Démonstration :
On sait que : \([QP] \) est le symétrique de \([AB]\) par rapport à \(d\).
Or : la symétrie axiale conserve les longueurs.
Donc : \(QP=AB=5cm\).
Question 4
Dans la figure ci-contre, on donne : \(N\) est le milieu de \([AD\)],
\(AD=6cm\), \(AB=5cm\), \(BC=2cm\), \(CD=5,5cm\), \(EF=1cm\), \(GH=0,5cm\) et \(ML=1,5cm\).
\(\widehat{ADC}=43°, \widehat{BCD}=110°, \widehat{DAB}=57\)° et \(\widehat{ABC}=102°\)
Quelle est la mesure de \(\widehat{ORQ}\) ?
On ne peut pas savoir.
110°
102°
57°
\(\widehat{ORQ}\) est le symétrique de… ?
La symétrie conserve les angles.
\(\widehat{ORQ}\) et son symétrique ont la même mesure.
\(\widehat{ORQ}\) est un angle obtus !
Démonstration :
On sait que : \(\widehat{ORQ}\) est le symétrique de \(\widehat{BCD} \) par rapport à \(d\).
Or la symétrie axiale conserve les angles.
Donc : \(\widehat{ORQ}=\widehat{BCD} =110°.\)
Question 5
Dans la figure ci-contre, on donne : \(N\) est le milieu de \([AD\)],
\(AD=6cm\), \(AB=5cm\), \(BC=2cm\), \(CD=5,5cm\), \(EF=1cm\), \(GH=0,5cm\) et \(ML=1,5cm\).
\(\widehat{ADC}=43°, \widehat{BCD}=110°, \widehat{DAB}=57\)° et \(\widehat{ABC}=102°\)
Quelle est la mesure de \(\widehat{ROP}\) ?
\(\widehat{ABC}\)
\(\widehat{DCA}\)
\(\widehat{CDA}\)
\(\widehat{ADC}\)
Quel est le sommet de \(\widehat{ROP}\) ?
Quels sont les symétriques de \(R, O\) et \(P\) ?
Quel est le symétrique du sommet \(O\) de \(\widehat{ROP}\) ?
Démonstration :
On sait que : \(R\) est le symétrique de \(C, O\) est le symétrique de \(D\) et \(P\) est le symétrique de \(A\) donc \(\widehat{CDA} \) (ou \(\widehat{ADC}\)) est le symétrique de \(\widehat{ROP} \) par rapport à \(d\).
Or la symétrie axiale conserve les angles.
Donc : \(\widehat{ROP} =\widehat{ADC}=43°\).