L'énoncé
Tu dois faire chaque question sur une feuille en t’aidant des astuces si tu as besoin. Ensuite tu peux faire afficher la correction de la question pour te corriger et pouvoir continuer l’exercice.
On considère dans cet exercice un triangle \(TRI\) équilatéral tel que \(TI\) = 6cm.
On admet que \(\widehat{TRI}=60°\).
Question 1
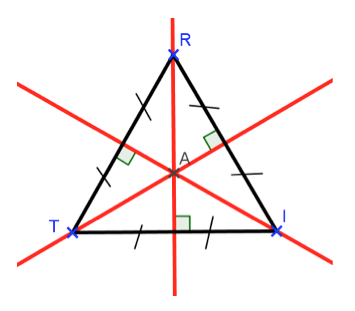
Trace le triangle \(TRI\) et son ou ses axe(s) de symétrie.
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur : on le trace à l’aide d’un compas.
Un triangle équilatéral admet 3 axes de symétrie.
Les axes de symétrie d’un triangle sont les médiatrices des côtés.
Question 2
On nomme \(A\) la point de concours des axes de symétrie du triangle \(TRI\).
Quelle est la mesure de \(\widehat{TIR}\) ? Démontre-le.
On sait qu'un triangle équilatéral admet trois axes de symétrie : les médiatrices des côtés : ici \((TA), (RA)\) et \((IA)\).
On sait aussi que \(\widehat{TIR}\) et \(\widehat{TRI}\) sont symétriques par rapport à \((TA)\), la médiatrice de \([RI]\).
Or la symétrie axiale conserve les angles.
Donc \(\widehat{TRI} = \widehat{TIR}= 60°.\)
Utilise la figure faite à la question 1.
Mesure \(\widehat{TIR}\) pour avoir une idée de ce que tu dois démontrer.
\(\widehat{TIR}\) et \(\widehat{TRI}\) sont symétriques par rapport à … ?
Utilise une propriété de la symétrie axiale.
Une démonstration se fait en 3 étapes : on sait que…, or…, donc…
Question 3
Quelle est la mesure de \(\widehat{TRA}\) ?
On sait que \((RA)\) est l'axe de symétrie de l'angle \(\widehat{TRI}\).
Or l'axe de symétrie d'un angle est sa bissectrice.
Donc \(\widehat{TRA} =\widehat{ARI} =\dfrac{1}{2} \widehat{TRI}=\dfrac{60°}{2}=30°\)
Donc \(\widehat{TRA} \) mesure \( 30°\).
Que représente \((RA)\) pour \(\widehat{TRI}\) ?
\((RA)\) est l’axe de symétrie de \(\widehat{TRI}\) et donc sa bissectrice.
\((RA)\) est la bissectrice de \(\widehat{TRI}\) signifie que \(\widehat{TRA} = \dfrac{1}{2} \widehat{TRI}\).
Question 4
On nomme \(T_1\) le point dintersection de \([RI]\) et de \((TA)\).
\(R_1\) le point dintersection de \([TI]\) et de \((RA)\).
\(I_1\) le point dintersection de \([TR]\) et de \((IA)\).
Détermine la longueur de \([TI_1]\).
\((II_1)\) est l'axe de symétrie de \(TRI\) issue de \(I\) donc \((II_1)\) est la médiatrice de \([TR]\)
Ainsi, \(I_1\) est le milieu de \([TR]\).
Donc on a : \(TI_1 = \dfrac{TR}{2}=\dfrac{6}{2}=3.\)
Finalement, \([TI_1]\) mesure 3 cm.
Que représente \((II_1)\) pour \([TR]\) ?
\((II_1)\) est la médiatrice de \([TR]\).
\(I_1\) est donc le … de \([TR]\) ?
\(I_1\) est le milieu de \([TR]\).
Question 5
Nomme tous les triangles rectangles de la figure.
\(TI_1I, \ TI_1A, \ RI_1I,\ RI_1A, \ RT_1A,\ RT_1T, \ IT_1A, \ IT_1T,\ IR_1A, \ IR_1R,\ TR_1A,\ TR_1R.\)
Les angles droits sont codés !
Il y a 12 triangles rectangles !