L'énoncé
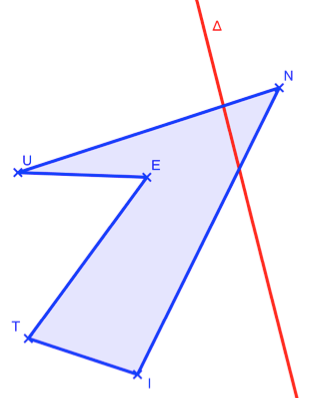
Dans cet exercice, on considère la figure suivante où :
\(UN=4cm\ ; UE=2cm \ ; ET=3,5cm \ ; TI=1,5cm\)
\(\widehat{UNI}=40°\ ; \widehat{NUE}=25°\ ;\widehat{UET}=55°\ ;\widehat{ETI}=75°.\)
Question 1
Reproduis la figure \(UNITE\) en respectant les données.
Fais d’abord une figure à main levée sur laquelle tu écris toutes les données numériques (longueurs et mesures d’angles).
Commence par exemple par construire \([UN]\) puis les angles \(\widehat{UNI}\) et \(\widehat{NUE}\).
Puis \([UE]\), puis \(\widehat{UET}\), puis \([ET]\) …
Question 2
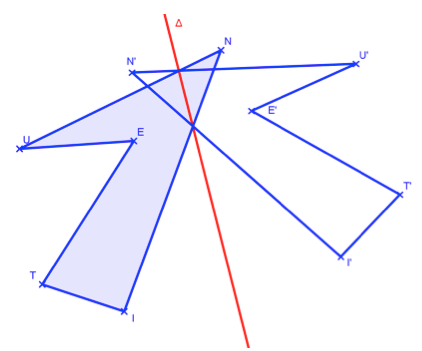
Construis le symétrique \(UNITE\) de \(UNITE\) par rapport à \(\Delta\).
Construis les symétriques de chaque sommet : \(U, N, I, T, E. \)
\(U’\) est le symétrique de \(U\) par rapport à \(\Delta\) signifie que \(\Delta\) est la médiatrice de \([UU’]\)…
Trace les segments \([U’N’]\) symétrique de \([UN], [N’I’]\) symétrique de \([NI]\)…
Si la figure est bien construite, \([UN]\) et son symétrique \([U’N’]\) sont sécants en un point de l’axe \(\Delta\). Et de même \([NI]\) et son symétrique \([N’I’]\) sont sécants en un point de l’axe \(\Delta\).
Question 3
Démontre que \(\widehat{E'T'I'}=75°\).
On sait que : \( \widehat{E'T'I'} \) est le symétrique de \( \widehat{ETI} \) par rapport à \(\Delta\) et \( \widehat{ETI} =75°\).
Or : La symétrie axiale conserve les angles.
Donc : \( \widehat{E'T'I'}=\widehat{ETI} =75° \)
Donc : \( \widehat{E'T'I'}\) mesure \(75°\).
Une démonstration se fait en trois étapes.
Les trois étapes sont : on sait que..., or…, donc…
Utilise la propriété de la symétrie sur les angles (conservés !)
Question 4
Quelle est la longueur de \([NU]\) ? Démontre-le.
On sait que : \([NU]\) est le symétrique de \([NU]\) par rapport à \(\Delta\) et que \(NU = 4cm\).
Or : La symétrie axiale conserve les longueurs.
Donc : \(NU=NU=4cm.\)
Tu peux mesurer sur ta construction pour avoir une idée…
\([N’U’]\) est le symétrique de… ?
La symétrie conserve les longueurs.
Une démonstration se fait en 3 étapes : on sait que, or, donc.
Question 5
Quelle est la mesure de \(\widehat{T'E'U'}\) ? Peux-tu le démontrer ?
On sait que \(\widehat{T'E'U'}\) est le symétrique de \(\widehat{UET}\) par rapport à \(\Delta\) et que \(\widehat{UET}=55°\).
Or la symétrie conserve les angles.
Donc : \(\widehat{T'E'U'}=\widehat{UET}=55°\)
Donc : \(\widehat{T'E'U'}\) mesure \(55°\).
Quel est le symétrique de \(\widehat{T'E'U'}\) ?
Tu peux le démontrer, de la même façon que pour la question 3.
\(\widehat{T'E'U'}\) est le symétrique de \(\widehat{UET}\) et \(\widehat{UET}=55°\).