L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
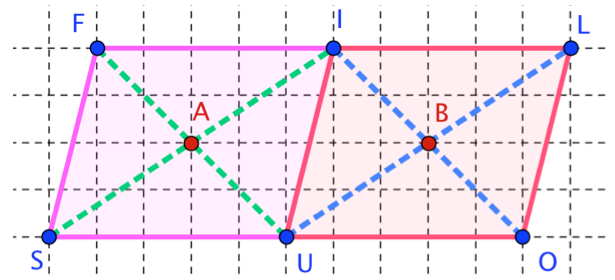
Les deux quadrilatères ci-dessous (en rose et rouge) sont deux parallélogrammes.
Le parallélogramme dessiné en rose peut se nommer :
\(SUIF\)
\(SUFI\)
\(SUFI\) n’est pas un nom correct pour cette figure car on passe du sommet \(U\) au sommet \(F\) en traversant le dessin en diagonale !
\(FIUS\)
\(FIUS\) est un nom correct pour cette figure car on part du sommet \(F \), puis on va vers \(I\), puis \(U\) et \(S\) pour finir !
\(SIFU\)
\(SIFU\) n’est pas un nom correct pour cette figure car on passe du sommet \(S\) au sommet \(I\) en traversant le dessin en diagonale !
Pour nommer le parallélogramme, on tourne autour de la figure, sans la traverser !
Retiens bien cette façon de nommer les quadrilatères ! On tourne autour de la figure, sans la traverser, et on peut tourner dans le sens qu’on veut !
Question 2
\([UI]\) est une diagonale du parallélogramme \(LOUI\).
\([UI]\) et \([IL]\) sont des côtés du parallélogramme.
\([UL]\) est une diagonale du parallélogramme \(LOUI\).
\([IL]\) est une diagonale du parallélogramme \(LOUI\).
\([UI]\) et \([IL]\) sont des côtés du parallélogramme.
\([IO]\) est un côté du parallélogramme \(LOUI\).
\([IO]\) est une diagonale du parallélogramme \(LOUI \).
Tu peux réviser les mots « côté » ou « diagonale » dans la vidéo ou la fiche sur les quadrilatères.
Ce vocabulaire est très important, et il faut bien l’apprendre ! Sur la figure, les segments en bleu et en pointillés sont les diagonales du parallélogramme \(LOUI\).
Question 3
On peut affirmer que \(B\) est le milieu de \([IO]\).
Il n’est pas certain que \(B\) soit le milieu de \([IO]\).
\(B\) n’est pas le milieu de \([UL]\).
\(B\) est le milieu de \([UL]\).
Les diagonales d’un parallélogramme se coupent en leurs … ?
Les diagonales d’un parallélogramme se coupent en leurs milieux (d’après le cours).
Les diagonales sont \([IO]\) et \([UL]\), et elles se coupent en \(B\) :
\(B\) est le milieu de \([IO]\) et le milieu de \([UL]\) !
Question 4
\(SU=FI\)
\([SU]=[FI]\)
\(SU=SF\)
\([SF]=[UI]\)
Quelles sont les propriétés des côtés opposés d’un parallélogramme ?
Les côtés opposés ont la même longueur.
Fais attention aux notations : \([SU]\) est le segment (le trait qui relie \(S\) et \(U\)), et \(SU\) est la longueur du segment.
Dans un parallélogramme, les côtés opposés ont la même longueur : ici \(SU=FI\) et \(SF=UI\). Mais attention, il ne faut pas mettre les crochets, qui servent uniquement à désigner les segments !
Fais attention aux notations : lorsque \(A\) et \(B\) sont deux points, \([AB]\) est le segment (le trait qui relie \(A\) et \(B\)), et \(AB\) est la longueur du segment.
Par exemple, pour dire que le segment \([AB]\) mesure 4 cm, on écrit que \(AB=4\ cm\) (et pas \([AB]=4\ cm\)).
Question 5
Les diagonales de \(FISU\) ont le même milieu.
Le quadrilatère en rouge \(FIUS) est un parallélogramme : ses diagonales se coupent en leurs milieux.
\((LO)\) est parallèle à \((SI)\).
\(SOLF\) est un parallélogramme.
\(SOLF\) est bien un parallélogramme, puisque grâce à la proposition 3 on sait qu’il a deux cotés parallèles (car \((LO)//(FS)\) ) : comme on a aussi \((SO)//(FL)\), le quadrilatère possède des côtés parallèles : c’est un parallélogramme !
\((LO)\) est parallèle à \((SF)\).
Vrai, pour le justifier on utilise une propriété des droites parallèles que tu as vu en classe : lorsque deux droites sont parallèles, toute parallèle à l’une est parallèle à l’autre. Ici comme \(UOLI\) (en rouge) est un parallélogramme donc ses côtés sont parallèles : \((LO)//(UI)\). De même comme \(SUIF\) (en rose) est un parallélogramme, on a \((UI)//(SF)\). Donc on en déduit que \((LO)\) est parallèle à \((SF)\).
Le quadrilatère en rouge se nomme-t-il \(UOIL\) ?
Les quadrilatères en rouge et en rose sont deux parallélogrammes : ils ont donc des côtés parallèles !
Ici on a fait deux démonstrations : une pour montrer que \((LO)\) est parallèle à \((SF)\) et une pour montrer que \(SOLF\) est un parallélogramme.
En classe de sixième, on commence à aborder ce type de raisonnement, tu peux reprendre la correction pour te familiariser avec cela !

En partant de \(S\) et en tournant bien autour du parallélogramme, on obtient le nom : \(SUIF\).