L'énoncé
Prends une page grand format pour cette figure, et place le segment à peu près au centre de la page.
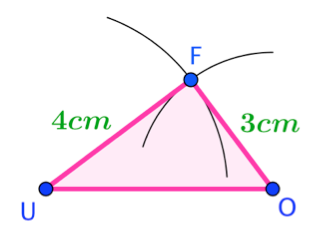
Pour commencer cet exercice, construis un segment \([UO]\) tel que \(UO=5\ cm\). 
Question 1
Construire le triangle \(FOU\) tel que \(OF=3\ cm\) et \(UF =4\ cm\).
La figure doit ressembler à cela :
Tu peux faire une figure à main levée pour avoir une idée de la forme du triangle \(FOU\).
Utilise ton compas : prends un écartement de 3 cm, et place la pointe du compas en \(O\). Trace alors un arc de cercle de rayon 3 cm.
Recommence la même opération en prenant un écartement de 4 cm et en mettant la pointe du compas en \(U\).
Question 2
Que remarques-tu sur le triangle \(FOU\) ? Quelle semble être sa nature ?
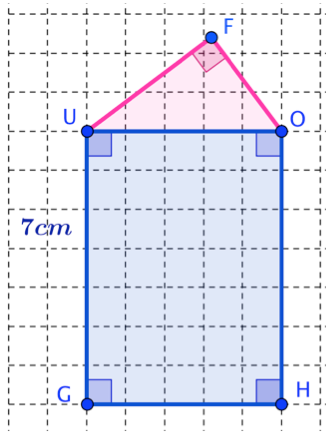
A l'aide de l'équerre, il semblerait que l'angle en \(F\) est un angle droit : on peut donc imaginer que le triangle \(FOU\) est un triangle rectangle.
Observe bien le triangle, il a une propriété bien particulière…
Un indice : prends une équerre !
Est-ce-qu’il y a un angle droit ?
Question 3
Construire à l'extérieur du triangle sur la même figure le rectangle \(UGHO\) tel que \(OH= 7\ cm\).
Fais une figure à main levée pour voir à quoi peut ressembler le rectangle !
Le rectangle va se placer sous le triangle.
En partant de \(O\), trace un segment de 7 cm vers le bas.
Question 4
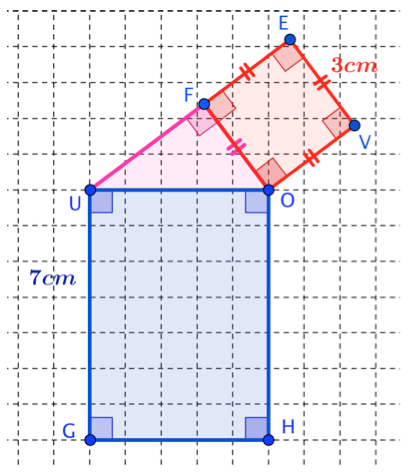
Construire à l'extérieur du triangle sur la même figure le carré \(FOVE\).
Là encore, figure à main levée à faire !
Quelle est la longueur du côté du carré ?
Un côté du carré est \([FO]\) tel que \(FO=3\ cm\).
On construit donc un carré de dimension 3 cm, dont l’un des côtés est \([FO]\) : utilise ton équerre et ta règle pour les mesures !
Question 5
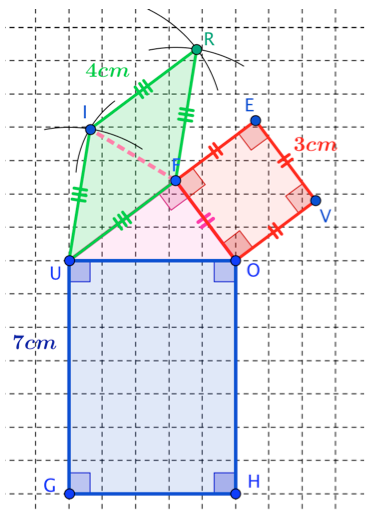
Construire à l'extérieur du triangle sur la même figure le losange \(FUIR\) tel que \(FI=3 \ cm\).
On construit pour commencer le triangle \(FUI\) : avec le compas, on prend un écartement de 3 cm et on place la pointe en \(F\) : on trace un premier arc de cercle.
Puis on prend un écartement de 4 cm et on met la pointe en \(F\) : on trace un deuxième arc de cercle. \(I\) est lintersection des deux arcs de cercle. On trace alors \(UFI\).
On place ensuite \(R\) en prenant un écartement de 4 cm et en mettant la pointe une fois en \(I\) et une fois en \(F\) !
Un schéma est nécessaire pour voir comment vont se placer à peu près les sommets \(R\) et \(I\).
\([FI]\) est une diagonale du losange.
Commence par placer \(I\) : on a \(FI= 3\ cm\) et \(UI=4\ cm\) puisque les côtés d’un losange ont tous la même longueur : utilise alors ton compas pour placer \(I\) !