Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Définition vectorielle des homothéties
I) Définition
Soient $O$ un point du plan et $k$ un réel non nul.
On appelle homothétie de centre $O$ et de rapport $k$ la transformation qui à tout point $M$ associe le point $M'$ tel que $\overrightarrow{OM'} = k \overrightarrow{OM}$.
Si on note $h$ l'homothétie de centre $O$ et de rapport $k$, les énoncés suivants sont équivalents.
$M'$ est l'image de $M$ par $h$
$M' = h(M)$
$\overrightarrow{OM'} = k \overrightarrow{OM}$
Exemples :
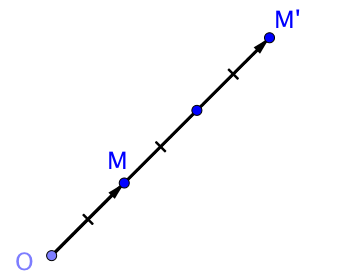
Dans cette figure, on a divisé le segment $[OM']$ en trois segments de même longueur égale à celle du segment $[OM]$.
Ainsi, on a $\overrightarrow{OM'} = 3 \overrightarrow{OM}$. C'est donc une homothétie de centre $O$ et de rapport $3$.
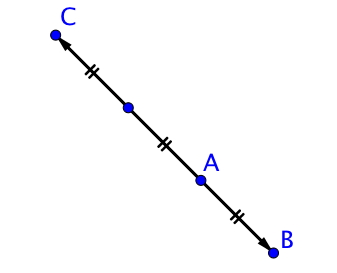
Sur le sc
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
