Le tableau ci-dessous présente la population du département des Bouches du Rhône en 2006 :
| Tranche d'âge | $[0;15[$ | $[15;30[$ | $[30;45[$ | $[45;60[$ | $[60;75[$ | $[75;90[$ | $[90;105[$ | Total |
| Nombre d'habitants | $346701$ | $377745$ | $400543$ | $387094$ | $261243$ | $149214$ | $15061$ | $1937601$ |
1) Quelle est la population, quelle est la variable, sa nature ?
2) Recopie et complète le tableau des fréquences cumulées croissantes (en pourcentage, arrondies à l’unité)
| Age | $0$ | $15$ | $30$ | $45$ | $60$ | $75$ | $90$ | $105$ |
| Fréquences cumulées |
3) Représente les fréquences cumulées dans un graphique avec des unités adaptées. Déduis-en la médiane et les quartiles de cette étude.
4) Donne une estimation de la moyenne en expliquant ta démarche.
La population est celle des Bouches du Rhône en 2006. La variable est la tranche d'âge.
On calcule les fréquences en divisant les effectifs par l’effectif total, puis on multiplie par $100$ pour les avoir en pourcentage, et on les cumule. On obtient le tableau :
| Age | $0$ | $15$ | $30$ | $45$ | $60$ | $75$ | $90$ | $105$ |
| Fréquences cumulées | 0 | 18 | 37 | 58 | 78 | 92 | 99 | 100 |
On obtient la représentation graphique suivante :
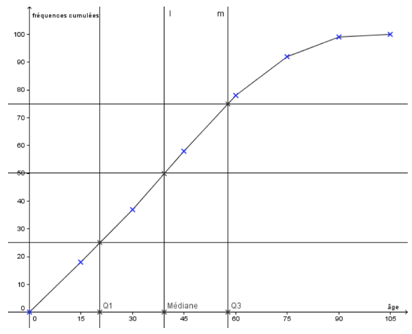
Ce qui permet, par lecture graphique, d’obtenir environ $20$ ans pour le premier quartile (correspondant à au moins $25%$ des valeurs de la série), $40$ ans pour la médiane (correspondant à au moins $50%$ des valeurs de la série) et $55$ ans pour le troisième quartile (correspondant à au moins $75%$ des valeurs de la série).
Pour calculer la moyenne, on remplace chaque intervalle par son centre, et on obtient environ $40$ ans.
Par exemple, il y a $18%$ des effectifs entre $0$ et $15$ ans. Le centre de la classe est $7,5$.
On pourra donc calculer la moyenne de la façon suivante : $m = 0.18 \times 7.5 + ... + ... + 0.01 \times 97.5$
Pour le dernier terme, il n’y a en effet que $1%$ des effectifs entre $90$ et $105$ ans dont le centre de la classe est $97,5$.
