Voici les notes d’un devoir noté sur 10
|
Note |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Total |
|
Effectif |
3 |
7 |
0 |
0 |
1 |
2 |
2 |
10 |
4 |
0 |
2 |
31 |
1) Calcule la note moyenne de ce devoir. A partir de ce seul indicateur, que peut-on conclure sur la réussite de ce devoir ?
2) Détermine la note médiane de ce devoir. A partir de ce seul indicateur, que peut-on conclure sur la réussite de ce devoir ?
3) Certaines notes sont explicables comme suit :
- Les deux personnes qui ont eu 10 ont triché mais ne se sont pas faits prendre.
- Les trois personnes qui ont eu 0 ont triché mais se sont faits prendre.
- Les sept personnes qui ont eu 1 reviennent d’une épidémie de grippe et avaient manqué tous les cours.
Que peut-on proposer pour calculer une nouvelle moyenne qui reflètera davantage le niveau de la classe sur ce devoir ? Fais ce calcul.
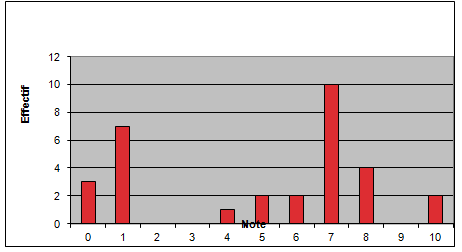
4) Représente le tableau à l’aide d’un diagramme en barres.
1) $M = \dfrac{3\times 0 + 7\times 1 + 1 \times 4 + 2 \times 5 + 2 \times 6 + 10 \times 7 + 4 \times 8 + 2 \times 10}{31}= 5$
La réussite de la classe semble plutôt moyenne.
2) L’effectif total étant de $31$, qui est impair, la médiane est au rang n°16 (cf. cours).
Regardons la 16ème note. Elle est de $7$ donc $Me = 7$.
La médiane est de $7$, cela signifie qu’au moins la moitié des élèves ont eu $7$. Le devoir est plutôt bien réussi. (En fait, les dix notes en dessous de 1 « baissent » la moyenne de la classe.)
3) Il paraît difficile de tenir compte des tricheurs (comment évaluer une performance si elle est faussée ?) et des résultats des malades (cela ne les excuse pas, mais on peut les comprendre…).
Donc « élaguons » ces notes et calculons une moyenne élaguée :
$\dfrac{4\times 1 + 5 \times 2 + 6 \times 2 + 7 \times 10 + 8 \times 4}{19} \approx 6,75$.
Cela reflète davantage le niveau de la classe sur ce devoir. Car avec une moyenne de presque $7$, le devoir semble réussi, ce qui est confirmé par la médiane.
4) Voici le diagramme en barres :