L'énoncé
Cet exercice est un QCM ; il n’y a qu’une seule bonne réponse possible parmi toutes celles proposées.
Tu as obtenu le score de
Question 1
Ce diagramme représente les fréquences (en nombre décimal) en fonction des valeurs d'un caractère.
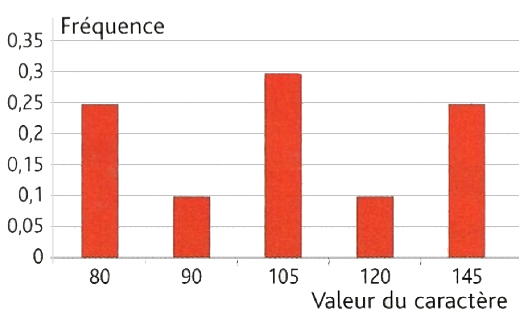
Calculez la moyenne de la série.
\(\overline{x} = 108\)
\(\overline{x} = 108,75\)
\(e = 0,3\)
On ne peut pas savoir.
Le calcul de la moyenne à partir des fréquences est identique à celui fait à partir des effectifs.
Le 1er rectangle rouge montre que 0,25 (ou 25%) des personnes ont le caractère 80.
\(\overline{x} = 80\times 0,25 + …\)
Question 2
Ce tableau représente le nombre de fichiers mp3 installés dans les lecteurs mp3 des élèves d'une classe de 20 élèves.
La moyenne des fichiers est :
\(\overline{x} = 116\)
\(\overline{x} = 79,5\)
le centre de la classe \([0;10[\) est 5, le centre de la classe \([10;50[\) est 30, le centre de la classe \([50;100[\) est 75, etc. Ensuite on fait la moyenne de la série :
\(\overline{x} = 5 \times 0,1 + 30 \times 0,3 + 75 \times 0,4 + 200 \times 0,2 = 79,5\)
\(\overline{x} = 43\)
On ne peut pas savoir.
On a ici une série regroupée par classe.
Quel est le centre de chaque classe ?
Par quoi faudra-t-il multiplier chaque fréquence ?
Comment se fait alors le calcul de la moyenne ?
Question 3
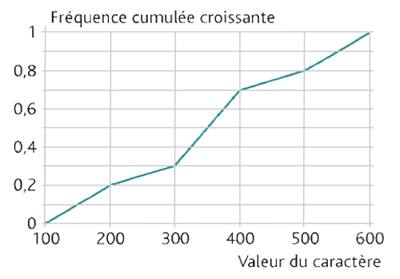
On a représenté ci-contre les fréquences cumulées croissantes d'une série statistique. Les fréquences ne sont pas en pourcentage ; le total est donc de 1.
Alors :
\(Q_1 = 300\)
\(Me = 0,3\)
\(Q_3 = 450\)
Par la même méthode, on obtiendrait par exemple que le premier quartile est d’environ 250 (on place cette fois 0,25 sur l’axe des ordonnées, on rejoint la courbe, et on lit l’abscisse correspondante).
Tout est impossible
\(Q_1\) correspond à une fréquence de 25% ou de 0,25.
Lire graphiquement la valeur correspondant à 0,25 et donc la valeur de \(Q_1\).
\(Me\) correspond à une fréquence de 50% ou de 0,5 ; lire alors graphiquement la valeur de \(Me\).
Lire graphiquement la valeur correspondant de \(Q_3\).
Question 4
Pour les questions 4 et 5 on se reportera à l'énoncé suivant :
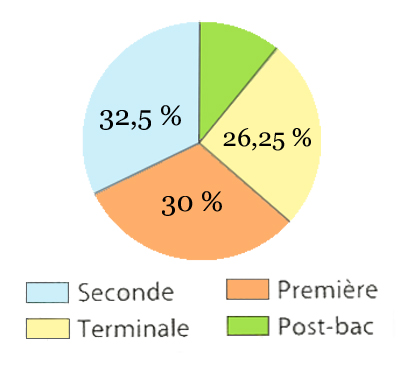
Ce diagramme représente la répartition des élèves d'un lycée qui accueille 286 élèves en seconde.
Le nombre d'élèves du lycée est de :
$781$
$858$
$880$
Donc \(N = 286 \times \dfrac{100}{32,5} = 880\).
On ne peut pas savoir.
Les $286$ élèves de seconde représentent 32,5% des élèves du lycée.
Combien d'élèves représentent les 100% des élèves du lycée ?
Question 5
La proportion "\(\dfrac{post-bac}{première}\)" est :
\(\dfrac{1}{3}\)
\(\dfrac{3}{7}\)
\(\dfrac{3}{8}\)
On ne peut pas savoir.
Quel est le pourcentage d'élèves en "post-bac" ?
Quel est le pourcentage d'élèves en "première" ?
Quel est le rapport demandé ?
Question 6
On considère la série suivante :
Lequel des graphiques suivants lui est associé ?
De plus, la hauteur du rectangle est alors de 10 unités, ce qui donne au total 30 petits carrés bleus (sachant que d’après la légende, 1 petit carré bleu = 0,01), soit une fréquence égale à \(30 \times 0,01 = 0,3\) : cela correspond bien à la première colonne du tableau. On vérifie de même que les autres colonnes sont bien représentées.
Aucun des graphiques proposés.
La classe [3 ; 6[ n'a pas la même amplitude que la classe [6 ; 11[. Cela doit se voir sur le graphique.
Les fréquences sont-elles cumulées croissantes ?
Question 7
On a représenté sur un axe les intervalles interquartiles et la médiane de deux séries statistiques.
Laquelle de ces propositions est vraie ?
Les valeurs de la série 1 sont inférieures aux valeurs de la série 2.
50% au moins des valeurs de la série 2 sont inférieures à 7.
75% au moins des valeurs de la série 1 sont inférieures à 5.
Le graphique de la série 1 permet en effet d’affirmer que : \(Q_1 = 2, Me = 3\) et \(Q_3 = 5\).
On ne peut pas savoir.
La représentation donne-t-elle une indication sur la valeur maximale de chaque série ?
Que vaut \(Me\) pour la série 2 ? Quelle interprétation peut-on en faire ?
Que vaut \(Q_3\) pour la série 1 ? Quelle interprétation peut-on en faire ?
Question 8
Ce nuage de points représente les fréquences cumulées croissantes d'une série statistique constituée par les salaires mensuels, en centaines d'euros, des salariés d'une entreprise.
Trois-quarts des salaires mensuels sont inférieurs à 1 900 €.
La moitié au moins des salaires mensuels sont supérieurs ou égaux à 1 900 €.
La moitié au moins des salaires mensuels est comprise entre 1 600 € et 2 000 € inclus.
On ne peut pas savoir.
Quelle fréquence correspond à un salaire de 1 600 € ? De 2 000 € ? Quel est le pourcentage de salariés gagnant entre 1 600 € et 2 000 € ?
Lire le salaire correspondant à une fréquence de 0,5 (la moitié).
Trois-quarts correspond à une fréquence de 0,75. Lire le salaire correspondant à une fréquence de 0,75.
Question 9
Ce diagramme représente le nombre de buts marqués par match pour une équipe de football.
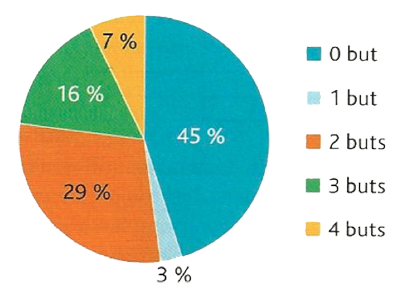
Le nombre moyen de buts marqués par match lors de la saison est :
\(\overline{x} = 1,37\)
\(\overline{x} = 0,5\)
\(\overline{x} = 2\)
On ne peut pas savoir.
C'est un calcul de moyenne à l'aide des fréquences (données ici en pourcentage).
Question 10
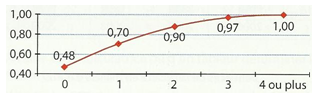
Voici la courbe des fréquences cumulées croissantes du nombre d'enfants moyen par famille en France en 2007.
On peut affirmer que :
3% des familles ont au plus 3 enfants.
90% des familles ont au moins 2 enfants.
70% des familles ont au moins 1 enfant.
22% des familles ont un enfant unique.
Comment trouver le pourcentage de famille qui n'a qu'un seul enfant ?
Que signifie de même le 0,90 ? Et le 0,70 ?
Le 0,97 signifie que 97% des familles ont de 0 à 3 enfants. Combien les 3% restant ont-ils d'enfants ?
Le graphique donne les fréquences cumulées croissantes.
Remarque : attention à bien différencier :"au plus", "au moins" etc.