L'énoncé
Exercice : Les statistiques de sportifs
On a étudié la fréquence cardiaque au repos (FCR) d'un groupe de 70 sportifs amateurs hommes et femmes.
Les résultats de cette étude sont récapitulés dans le tableau ci-dessous :
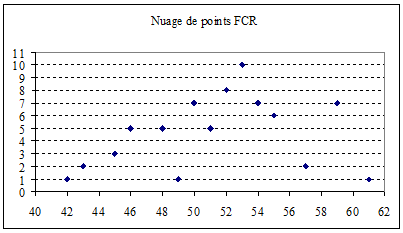
| FCR | 42 | 43 | 45 | 46 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 57 | 59 | 61 |
| Effectif | 1 | 2 | 3 | 5 | 5 | 1 | 7 | 5 | 8 | 10 | 7 | 6 | 2 | 7 | 1 |
Question 1
Quels sont le caractère et la population étudiés ?
La population étudiée est "les 70 sportifs" et le caractère étudié est "la FCR".
Ne confondez pas population et caractère.
Le caractère est une caractéristique d'une population !
Question 2
Calculer l'étendue et préciser le mode de cette série en justifiant votre démarche.
L'étendue est la différence entre la plus grande et la plus petite valeur : \(e = 61 -42 = 19\)
Le mode est la valeur correspondant au plus grand effectif donc ici il est de 53.
C'est du cours mais ne confondez pas les nombres à soustraire. On cherche des renseignements sur la FCR.
Question 3
Déterminer le pourcentage à 0,1 près de sportifs ayant une FCR d'au plus 45.
Il y a 6 sportifs ayant une FCR d'au plus 45 (en effet il y en a 1 + 2 + 3).
Or, \(\dfrac{6}{70} \times 100 \approx 8,6\)
Ainsi, 8,6% des sportifs ont une FCR d'au plus 45.
Combien y a-t-il de sportifs en tout ?
Combien de sportifs ont une FCR d'au plus 45 ?
"D'au plus 45" ne signifie pas "de plus de 45".
Question 4
Déterminer le pourcentage à 0,1 près de sportifs ayant moins de 53 de FCR.
Il y a 37 sportifs ayant une FCR de moins de 53.
\(\dfrac{37}{70} \times 100 \approx 52,9\)
52,9% des sportifs ont moins de 53 de FCR.
Combien de sportifs ont moins de 53 de FCR ?
Avoir 53 de FCR n'est pas avoir moins de 53 de FCR.
Question 5
Calculer la moyenne et déterminer la médiane et le 1er quartile en utilisant ta calculatrice.
Déterminer en le justifiant le troisième quartile.
Calcul de la moyenne :
\(\overline{x} =\dfrac{1 \times 42 + 2 \times 43 + ... + 7 \times 59 + 1 \times 61}{70}\)
Donc \(\overline{x} \approx 51,8\)
Médiane et premier quartile, à la calculatrice on obtient :
\(Q_1 = 50\)
\(Me = 52\)
Troisième quartile :
Il y a \(N = 70\) valeurs.
\(\dfrac{3}{4} \times N = \dfrac{3}{4} \times 70 = 52,5\)
Donc \(Q_3\) est la 53e valeur : \(Q3 = 54\)
C'est du cours !
Vous devez savoir utiliser les listes de votre calculatrice ; se reporter au manuel si besoin.
Pour la médiane et les quartiles, il peut être nécessaire d'utiliser les effectifs cumulés croissants.
Question 6
Quel est l'intervalle interquartile ? Quel pourcentage de sportifs a une FCR comprise dans cet intervalle ? Quel est l'écart interquartile ?
L'intervalle interquartile est \([Q_1 ; Q_3]\) soit \([50 ; 54]\).
50% des sportifs ont une FCR comprise dans cet intervalle.
L'écart interquartile est \(Q_3 - Q_1 = 54 - 50 = 4\)
C'est du cours !
Ici nul besoin d'effectuer un calcul de pourcentages ; vous devez avoir compris l'interprétation des quartiles.
Question 7
Recopier et compléter ces phrases :
« 50% des sportifs ont moins de ... de FCR. »
« Les sportifs de moins de 54 de FCR représentent ... du total des sportifs. »
Phrase 1 : 50% fait immédiatement penser à la médiane qui est de 52 donc : « 50% des sportifs ont moins de 52 de FCR. »
Phrase 2 : 54 de FCR fait immédiatement penser à Q3 qui est de 54 donc : « Les sportifs de moins de 54 de FCR représentent 75% du total des sportifs. »
Ici nul besoin d'effectuer de calculs de pourcentages ; vous devez avoir compris l'interprétation des quartiles.
Question 8
Tracer le nuage de points de cette série sur du papier millimétré.
En abscisse figurent les FCR. Inutile de commencer la graduation à 0 ; on peut la débuter à 40.
En ordonnée figurent les effectifs ; regardez votre tableau pour voir quelles sont les valeurs prises par les effectifs et adapter votre graduation.
Pensez à légender vos graphiques.
Question 9
Dans le tableau 2 ci-dessous, regrouper les effectifs par classes d'amplitude 5.
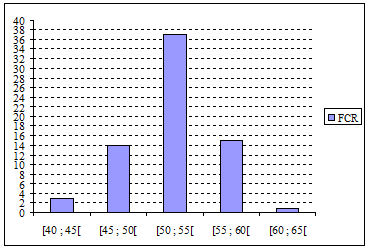
Tracer l'histogramme correspondant sur du papier millimétré.
Calculer à nouveau la moyenne en utilisant la répartition par classes.
Le résultat obtenu est-il le même que lors du calcul précédent ? Est-il plus fiable ?
| FCR | [ 40 ; ... [ | ... | ... | ... | ... | Total |
| Effectif |
| FCR | [ 40 ; 45 [ | [ 45 ; 50 [ | [ 50 ; 55 [ | [ 55 ; 60 [ | [ 60 ; 65 [ | Total |
| Effectif | 3 | 14 | 37 | 15 | 1 | 70 |
Histogramme :
Le centre de la classe \([40 ; 45[\) est : \(\dfrac{45+40}{2}=42,5\).
On en déduit que :
\(\overline{x} = \dfrac{3 \times 42,5 + 14 \times 47,5 + 37 \times 52,5 + 15 \times 57,5 + 1 \times 62,5}{70}\)
\(\overline{x} = \dfrac{3660}{70}\) donc \(\overline{x} \approx 52,285\)
Le résultat obtenu est différent de celui obtenu au calcul précédent. Il est moins fiable du fait des classes.
L'amplitude de la classe \([40 ; 45[\) est \(45 – 40 = 5\).
Une personne qui aurait 45 de FCR ne doit pas être comptabilisée dans la classe \([40 ; 45[\).
Pour l'histogramme vérifiez bien que vos classes ont la même amplitude.
Pour le calcul de la moyenne pensez aux centres de chaque classe.
Question 10
Compléter le tableau de la question 4 avec la distribution des fréquences en pourcentages à 1% près et avec les fréquences cumulées croissantes.
Dans quelle classe se situe la médiane ? Justifier.
| FCR | [ 40 ; 45 [ | [ 45 ; 50 [ | [ 50 ; 55 [ | [ 55 ; 60 [ | [ 60 ; 65 [ | Total |
| Effectif | 3 | 14 | 37 | 15 | 1 | 70 |
| Fréquence en % | 4 | 20 | 53 | 22 | 1 | 100 |
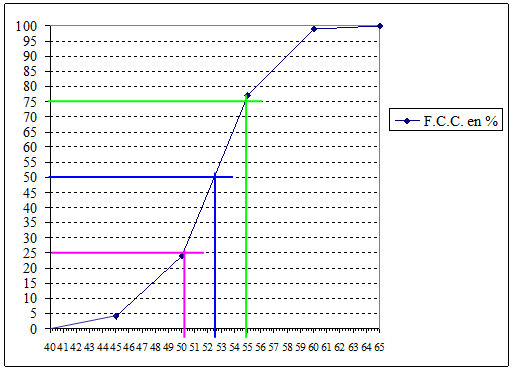
| F.C.C. en % | 4 | 24 | 77 | 99 | 100 |
Pour la classe [ 40 ; 45 [, l'effectif est de 3.
\(\dfrac{3}{70}\times 100\approx 4,2\) donc la fréquence en % associée est de 4.
D'après les F.C.C., on constate que 24% des sportifs ont une FCR dans la classe \([45 ; 50[\) et 77% dans la classe \([50 ; 55[\).
La médiane se situe donc dans la classe \([50 ; 55[\).
Le calcul de chaque fréquence revient à un calcul de pourcentage.
La médiane sépare la série en deux groupes de même taille ; elle correspond à 50% de l'effectif.
Question 11
Tracer le polygone des fréquences cumulées croissantes sur du papier millimétré.
Déterminer graphiquement une valeur approchée de la médiane, et des premier et troisième quartiles. (Laisser apparents les traits de construction et répondre par une phrase !)
Graphiquement une valeur approchée de la médiane est 52,5 de \(Q_1\) est 50 et de \(Q_3\) est 55.
En abscisse, inutile de commencer la graduation à 0 ; on peut la débuter à 40.
En ordonnée, ne pas hésiter à graduer de 5 en 5 pour une meilleure lecture.
La médiane correspond à 50% de l'effectif, on lit donc la FCR correspondante sur le graphique. Idem pour \(Q_1\) et \(Q_3\).