L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
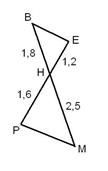
On considère la figure suivante. On veut savoir si les droites \((BE)\) et \((PM)\) sont parallèles. Quelle propriété va-t-on tester ?
La propriété de Thalès.
La réciproque de la propriété de Thalès.
La propriété de Pythagore.
Aucune des trois réponses précédentes n’est exacte.
Pour le parallélisme de deux droites, vous ne connaissez pas beaucoup de propriétés.
Question 2
Les points \(B\), \(H\), \(M\) et \(E\), \(H\), \(P\) sont alignés dans le même ordre, on compare donc les rapports \(\dfrac{HE}{HP}\) et \(\dfrac{HB}{BM}\).
On a : \(\dfrac{HE}{HP}=\dfrac{12}{16}=\dfrac{3}{4}\) et \(\dfrac{HB}{BM}= \dfrac{18}{25}\)
Les droites \((PE)\) et \((HM)\) sont donc :
Sécantes d’après la réciproque de la propriété de Thalès.
Sécantes d’après la contraposée de la propriété de Thalès.
Parallèles d’après la réciproque de la propriété de Thalès.
Aucune des trois réponses précédentes n’est exacte.
Savez-vous utiliser la propriété réciproque de Thalès ? Sinon, allez voir la vidéo dans les prérequis.
Si les rapports ne sont pas égaux, peut-on utiliser la réciproque ?
Question 3
Soit un repère orthonormé. On considère les points : \(A (1 ; 5), B (- 3 ; 1), C (8 ; - 2)\).
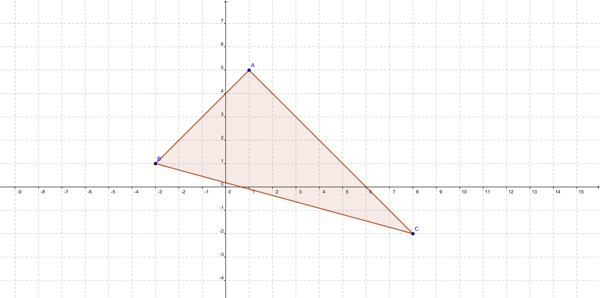
Calculez les longueurs des côtés du triangle \(ABC\).
\(AB= \sqrt{32} ; AC= \sqrt{49} ; BC= \sqrt{112}\)
\(AB= \sqrt{32} ; AC= \sqrt{98} ; BC= \sqrt{112}\)
\(AB= \sqrt{32} ; AC= \sqrt{98} ; BC= \sqrt{130}\)
Aucune des trois réponses précédentes n’est exacte.
Utilisez la formule du cours donnant la distance entre deux points.
Question 4
On sait que : \(A (1 ; 5), B (- 3 ; 1), C (8 ; - 2)\)
\(AB= \sqrt{32} ; AC= \sqrt{98} ; BC= \sqrt{130}\)
Quelle est la nature du triangle \(ABC\) ?
\(ABC\) est isocèle non rectangle.
\(ABC\)est rectangle non isocèle.
\(ABC\) est rectangle et isocèle.
Aucune des trois réponses précédentes n’est exacte.
Peut-il être isocèle ? Équilatéral ? Rectangle ?
Il va falloir utiliser la réciproque de Pythagore pour conclure.
Question 5
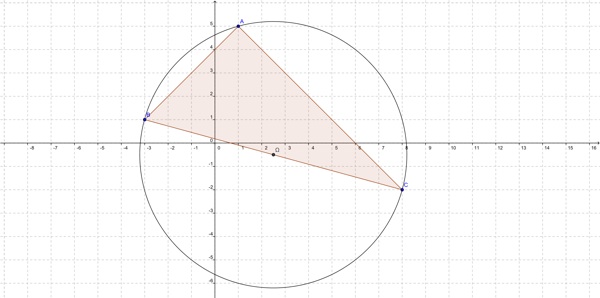
\(A (1 ; 5), B (- 3 ; 1), C (8 ; - 2)\)
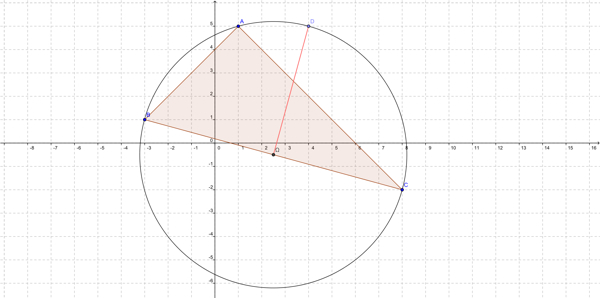
Déterminez les coordonnées du centre \(\Omega\) et le rayon R du cercle circonscrit au triangle ABC.
\(\Omega (\dfrac{5}{2} ; -\dfrac{1}{2})\) et \(R = \dfrac{\sqrt{130}}{2}\)
\(\Omega (\dfrac{5}{2} ; -\dfrac{1}{2})\) et \(R = \dfrac{\sqrt{98}}{2}\)
\(\Omega (-\dfrac{11}{2} ; -\dfrac{1}{2})\) et \(R = \dfrac{\sqrt{130}}{2}\)
Aucune des trois réponses précédentes n’est exacte.
Savez-vous où se trouve le centre du cercle circonscrit à un triangle rectangle ?
Revoyez la vidéo associée si vous en avez besoin.
Il se trouve au milieu de l’hypoténuse. C’est donc le milieu de \([CB]\).
Question 6
Montrez que le point \(D (4 ; 5)\) appartient au cercle circonscrit du triangle \(ABC\).
\(\Omega D = \dfrac{\sqrt{130}}{2}\) mais cela ne prouve rien.
\(\Omega D = \dfrac{\sqrt{130}}{2}\) et \(D\) appartient au cercle.
\(\Omega D = \dfrac{\sqrt{130}}{2}\) donc \(D\) n’appartient pas au cercle.
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous la définition d’un cercle ? Faites vous un brouillon. Placez un point \(D\) sur ce cercle.
\(D\) est sur le cercle si et seulement si \(\Omega D = R\).
Vous devez donc calculer la longueur \(\Omega D\) et la comparer au rayon.
Question 7
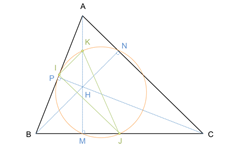
Soit \(ABC\) un triangle quelconque. On appelle \(M\), \(N\) et \(P\) les pieds des hauteurs de \(ABC\) issues respectivement des sommets \(A\), \(B\) et \(C\). Soit \(H\) l'orthocentre de \(ABC\).
On appelle enfin \(I\), \(J\) et \(K\) les milieux respectifs des segments \([AB]\), \([BC]\), \([AH]\).
On veut démontrer que le point \(M\) appartient au cercle \(C\) de diamètre \([JK]\). (Question 7 et 8) Quelle est la première étape de la démonstration ?
On montre que \(M\) est le pied de la hauteur issue de \(A\).
On montre que \(JKM\) est un triangle rectangle.
On note \(X\) le milieu de \([IJ]\) et on montre que \(XM = XJ = XI\).
Aucune des trois réponses précédentes n’est exacte.
Il serait pratique de montrer que le cercle est circonscrit au triangle \(KJM\).
On saurait ainsi que \(M\) appartient au cercle.
Question 8
Sachant que \(JKM\) est un triangle rectangle, on peut donc affirmer que :
\(M\) appartient au cercle de diamètre \([KJ]\) car le triangle \(KJM\) est rectangle en \(M\) et il est donc inscrit dans le cercle de diamètre \([IJ]\).
\(M\) appartient au cercle de diamètre \([KJ]\) car \(P\), \(M\) et \(N\) sont aussi sur le cercle.
\(M\) appartient au cercle de diamètre \([KJ]\) car on sait que \(M\), \(K\) et \(J\) sont à la même distance du centre du cercle.
Aucune des trois réponses précédentes n’est exacte
Connaissez-vous la particularité d’un triangle inscrit dans un cercle dont un des côtés est un diamètre ?
Question 9
On veut à présent montrer que I appartient aussi au cercle de diamètre \([JK]\).
Pour cela, on pourrait montrer que \((IK)\) et \((BN)\) sont parallèles. Quel théorème va t-on utiliser ?
La propriété de Thalès dans le triangle \(ABN\).
La propriété de Pythagore dans le triangle \(ABN\).
La propriété de la droite des milieux dans le triangle \(ABH\).
Aucune des trois réponses précédentes n’est exacte.
La droite \((BN)\) est aussi la droite \((BH)\).
Travaillez dans le triangle dont on connait des milieux de côtés.
Question 10
On sait que \((IK)\) et \((BN)\) sont parallèles. Pour les mêmes raisons, dans le triangle \(ABC\), on montre que \((IJ)\) est parallèle à \((BC)\). Que peut-on en déduire pour les droites \((IK)\) et \((IJ)\) ?
Elles ont parallèles.
Elles sont perpendiculaires.
On ne peut pas savoir.
Aucune des trois réponses précédentes n’est exacte.
Comparez les angles \(\widehat{KIJ}\) et \(\widehat{BNC}\).
Question 11
On sait désormais que \(IJK\) est rectangle en \(I\). Le point \(I\) appartient au cercle de diamètre \([KJ]\) car le triangle \(IJK\) est rectangle en \(I\) et il est donc inscrit dans le cercle de diamètre \([IJ]\).
On vient de montrer que les points \(I\), \(J\), \(K\), \(M\) sont sur un même cercle. On dit qu'ils sont :
Cocycliques.
Cocercliques.
Colinéaires.
Aucune des trois réponses précédentes n’est exacte.
Le mot copain, (co-pain) signifie partager le pain. Comment partager alors le même cercle ? Attention à utiliser le bon adjectif.