L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
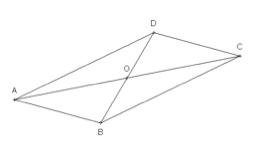
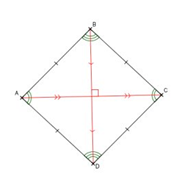
Question 1
À quelle condition \(ABCD\) est-il un parallélogramme ?
\(AC = BD\)
\(OA = OB = OC = OD\)
\(O\) est le milieu de \([AC]\) et de \([BD]\).
Aucune des trois réponses précédentes n’est exacte.
Avez-vous besoin d’un rappel sur le parallélogramme ? Allez voir la vidéo de rappel.
C’est une figure centrale de vos années lycée en géométrie. Prenez le temps de tout savoir d’elle.
Question 2
\(ABCD\) est un rectangle, si et seulement si : 
Ses diagonales ont le même milieu.
Ses diagonales ont la même longueur.
Ses diagonales ont le même milieu et la même longueur.
Aucune des trois réponses précédentes n’est exacte.
On cherche ici une condition nécessaire et suffisante.
Si vous trouvez un contre-exemple, la proposition est fausse.
Question 3
\(ABCD\) est un losange, si et seulement si :
Il n’a pas d’angle droit.
C’est un parallélogramme sans angle droit.
C’est un carré sans angle droit.
Aucune des trois réponses précédentes n’est exacte.
Savez-vous définir une figure en disant ce qu’elle n’a pas ?
La liste pourrait être longue.
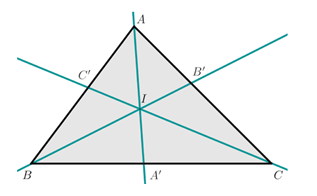
Question 4
Comment appelle-t-on le point d'intersection des médianes d'un triangle ?
Le centre du cercle circonscrit au triangle.
Le centre de gravité du triangle.
Le centre du cercle inscrit au triangle.
Aucune des trois réponses précédentes n’est exacte.
On a tracé une médiane sur la figure. Tracez les deux autres sur un brouillon.
Ce point est souvent appelé \(G\)…
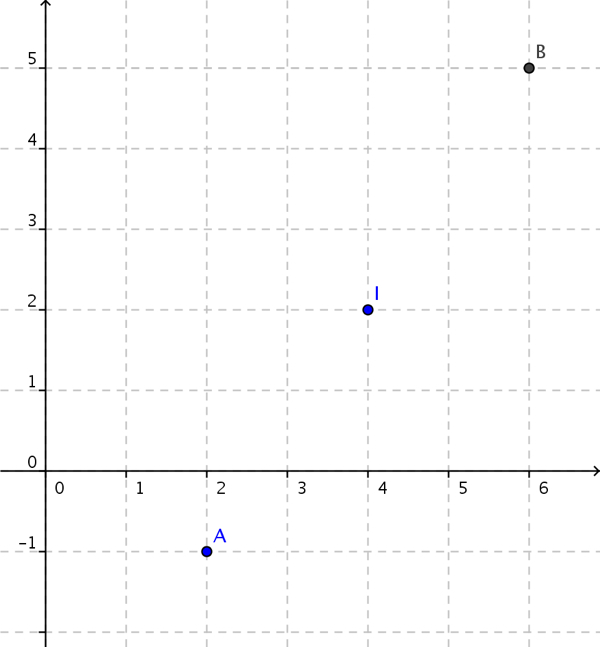
Question 5
Dans un repère orthonormé, On considère les points \(A(x_A;y_A )\) et \(B(x_B;y_B)\).
Quelle est la formule de la longueur \(AB\) ?
\(AB = \sqrt{(x_A-y_A)^2+(x_B-y_B)^2}\)
\(AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(AB = \sqrt{(x_B+x_A)^2+(y_B+y_A)^2}\)
Aucune des trois réponses précédentes n’est exacte.
Apprenez votre cours. Si besoin, vous pouvez revoir la vidéo dans les prérequis.
Question 6
On note \(I(x_I ; y_I)\) le milieu du segment \([AB]\).
Quelles sont ses coordonnées ?
\(\left\{ \begin{array}{rcl} y_I = \dfrac{x_B+x_A}{2} \\ x_I = \dfrac{y_B+y_A}{2} \end{array}\right.\)
\(\left\{ \begin{array}{rcl} x_I = \dfrac{x_B+x_A}{2} \\ y_I = \dfrac{y_B+y_A}{2} \end{array}\right.\)
\(\left\{ \begin{array}{rcl} x_I = \dfrac{x_B-x_A}{2} \\ y_I = \dfrac{y_B-y_A}{2} \end{array}\right.\)
Aucune des trois réponses précédentes n’est exacte.
L’abscisse de I est la moyenne des abscisses de \(A\) et de \(B\).
Savez-vous calculer la moyenne de deux nombres ?
C’est la demi-somme des deux nombres bien sûr.
Question 7
Dans un triangle, le point d'intersection des trois bissectrices est : 
Le centre du cercle inscrit au triangle.
L’orthocentre.
Le centre du cercle circonscrit au triangle.
Aucune des trois réponses précédentes n’est exacte.
Vous souvenez-vous de la notion de bissectrice ? Si non allez voir la vidéo dans les prérequis.
Ne confondez pas avec les médiatrices !
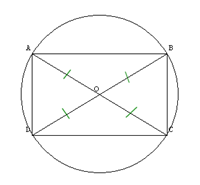
Question 8
Observez bien la figure suivante. Quelle est la nature de \(ABCD\) ?
Un carré.
Un losange.
Un rectangle.
Aucune des trois réponses précédentes n’est exacte.
La figure est trompeuse. Ne tenez compte que des renseignements donnés sur la figure.
Observez les propriétés des côtés ou des diagonales.
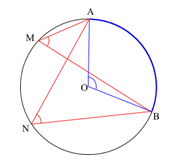
Question 9
Observez bien cette figure et cochez la bonne réponse.
\(2\widehat{MAO} = \widehat{MAB}\)
\(\widehat{AOB} = \widehat{AMB}\)
\(\widehat{ANB}= \widehat{AMB} \)
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous les propriétés des angles inscrits ? Vous pouvez revoir la vidéo dans les prérequis.
Les deux angles inscrits sont en rouge. Ils interceptent l’arc \(\overset{\frown}{AB}\).
Question 10
Dans un triangle \(ABC\), on considère la médiane \((AA')\). Le point \(G\), centre de gravité du triangle appartient au segment \([AA']\) et vérifie :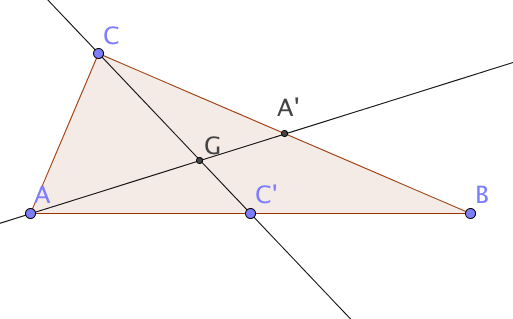 
\(GA = GA’\) (\(G\) est le milieu de \([AA’]\))
\(AG = \dfrac{1}{3} \times AA’\)
\(A’G = \dfrac{1}{3} \times AA’ \)
Aucune des trois réponses précédentes n’est exacte.
Oui mais en partant de quel point ? De \(A\) ou de \(A’\) ?
De \(A\).
On dit habituellement que le centre de gravité est au deux tiers de la médiane.