L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
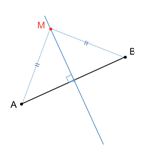
Soient \(A\) et \(B\) deux points distincts du plan.
Déterminez l'ensemble des points \(M\) vérifiant : \(AM + MB = AB\)
L’ensemble des points \(M\) est ici la droite \((AB)\).
L’ensemble des points \(M\) est ici le segment \([AB]\).
L’ensemble des points \(M\) est ici la médiatrice du segment \([AB]\).
Aucune des trois réponses précédentes n’est exacte.
Faites une figure pour vous aider. Placez des points \(M\) à différentes places.
Vous souvenez-vous de l’inégalité triangulaire ? Avec trois points du plan, on a toujours \(AM + MB \geq AB\).
Dans quel cas a t-on égalité ?
Question 2
Déterminez l'ensemble des points \(M\) vérifiant : \(AM - MB = 0\)
L’ensemble des points \(M\) est ici la médiatrice du segment \([AB]\).
L’ensemble des points \(M\) est ici le segment \([AB]\).
L’ensemble des points \(M\) est ici la droite \((AB)\).
Aucune des trois réponses précédentes n’est exacte.
\(AM - MB = 0 \Leftrightarrow AM = MB\), d’où \(MA = MB\)
Quelle est la nature du triangle ?
Question 3
Déterminez l'ensemble des points \(M\) vérifiant : \(AM^2 + MB^2 = AB^2\)
L’ensemble des points \(M\) est ici le segment \([AB]\).
L’ensemble des points \(M\) est ici la médiatrice du segment \([AB]\).
L’ensemble des points \(M\) est ici le cercle de diamètre \([AB]\).
Aucune des trois réponses précédentes n’est exacte.
Cette égalité doit vous faire penser à une propriété connue.
Pythagore bien sûr. Le triangle est donc rectangle en \(M\).
Faites une figure et tracez plusieurs triangles rectangles \(ABM\) sachant que \(A\) et \(B\) sont fixes.
Question 4
Déterminez l'ensemble des points \(M\) vérifiant :
\(\overrightarrow{AM} + \overrightarrow{MB} =\overrightarrow{AB}\)
L’ensemble des points \(M\) se restreint donc ici uniquement au point \(A\) et au point \(B\).
L’ensemble des points \(M\) est ici la médiatrice du segment \([AB]\).
L’ensemble des points \(M\) est donc ici le plan en entier (tous les points du plan vérifient cette relation).
Aucune des trois réponses précédentes n’est exacte.
Reconnaissez-vous ici une propriété connue ?
La relation de Chasles, non ? Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.
Question 5
Déterminez l'ensemble des points \(M\) vérifiant :
\(\overrightarrow{AM}-\overrightarrow{MB}=\overrightarrow{AB}\)
L’ensemble des points \(M\) est donc ici le plan en entier (tous les points du plan vérifient cette relation).
L’ensemble des points \(M\) est ici la médiatrice du segment \([AB]\).
L’ensemble des points \(M\) se restreint donc ici uniquement au point \(A\).
Aucune des trois réponses précédentes n’est exacte.
Utilisez la relation de Chasles pour modifier le terme de gauche. Exprimez \(\overrightarrow{BM}\) en fonction d’un vecteur fixe.
Si \(\overrightarrow{BM}=0\) alors que dire de \(B\) et \(M\) ?
Question 6
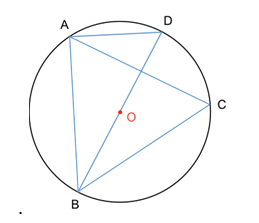
Soit \(ABC\) un triangle équilatéral. \(O\) est le centre de son cercle circonscrit \(C\).
\(D\) est le point du cercle \(C\) diamétralement opposé à \(B\).
Que représente la droite \((BD)\) pour le segment \([AC]\) ?
La droite \((BD)\) est la bissectrice du segment \([AC]\).
La droite \((BD)\) est la médiatrice du segment \([AC]\).
La droite \((BD)\) est le milieu du segment \([AC]\).
Aucune des trois réponses précédentes n’est exacte.
\(AB = BC\) car le triangle est... ?
\(OA = OC\) car … ?
\(O\) et \(B\) sont donc équidistants des extrémités du segment \([AB]\).
Un oubli sur cette notion ? Allez voir la vidéo dans les prérequis.
Question 7
On sait que dans un triangle équilatéral, médiatrices et bissectrices sont confondues.
On sait aussi que l'angle \(\widehat{ABC}\) mesure 60°.
Que mesure donc l'angle \(\widehat{ABD}\) ?
60°
30°
90°
Aucune des trois réponses précédentes n’est exacte.
Souviens toi : une bissectrice partage un angle en deux angles de même mesure.
Question 8
On a :
Les angles \(\widehat{ADB}\) et \(\widehat{ACB}\) sont égaux car ce sont des angles inscrits qui interceptent le même arc.
Les angles \(\widehat{ADB}\) et \(\widehat{ACB}\) sont égaux car ce sont des angles au centre qui interceprtent le même arc.
Les angles \(\widehat{ADB}\) et \(\widehat{ACB}\) ne sont pas égaux.
Aucune des trois réponses précédentes n’est exacte.
Savez-vous ce que sont des angles inscrits ? Allez voir la vidéo associée dans les prérequis.
Question 9
On sait désormais que \(\widehat{ADB}\) et \(\widehat{ACB}\) sont égaux et que \(\widehat{ADB}= \widehat{ACB}=60°\).
En notant à présent que \([BD]\) est un diamètre du cercle, quelle est la nature du triangle \(BAD\) ?
Il est rectangle en \(A\).
Il est isocèle en \(B\).
Il est équilatéral.
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous la particularité d'un triangle inscrit dans un cercle sachant qu'un de ses côtés est un diamètre ?
Vous pouvez revoir la vidéo de rappel dans les prérequis.
Question 10
Sachant que \(ABD\) est rectangle en \(A\) et que \(\widehat{ADB}=60°\), l'angle \(\widehat{ABD}\) mesure donc :
60°
45°
30°
Aucune des trois réponses précédentes n’est exacte.
Dans un triangle rectangle, les deux angles aigus sont complémentaires.
Cela signifie que la somme de leurs mesures vaut 90°.