L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle est la formule de l'aire d'un triangle $ABC$ ?
On notera : $a=BC$ et $b=AC$
$\dfrac{1}{2}ab\sin(\widehat{C})$
$\dfrac{1}{2}ab\sin(\widehat{A})$
$ab\sin(\widehat{C})$
Question 2
On note : $a=BC$ et $b=AC$
Comment comprendre ce choix de notation ?
En fonction du nom du segment
En fonction du jour de la semaine
En fonction de l'angle opposé
En effet, le longueur du segment $[BC]$, opposé à l'angle $\widehat{A}$, est appelée la longueur $a$.
Question 3
Quelle droite particulière du triangle utilise-t-on pour calculer son aire ?
La médiane
La hauteur
On utilise en effet la droite perpendiculaire à un côté et passant par le sommet opposé.
La médiatrice
Question 4
Quelle est la formule usuelle pour le calcul de l'aire d'un triangle ?
$\text{Base}\times \text{hauteur}$
$\dfrac{\text{Base}\times \text{hauteur}}{2}$
C'est en effet la formule que l'on utilise traditionnellement.
$\dfrac{abc}{3}$
Question 5
Dans la nouvelle formule du calcul de l'aire : $A=\dfrac{1}{2}ab\sin(\widehat{C})$
Quelle longueur jour le rôle de la base ?
$a$
$b$
On utilise en effet la base relative à $[AC]$.
$\sin(\widehat{C})$
Question 6
Quelle propriété particulière de la hauteur utilise-t-on ?
Sa perpendicularité
On se place en effet dans le triangle rectangle formé par la hauteur.
Le fait qu'elle passe par le milieu du segment
Le fait qu'elle coupe l'angle en deux moitiés égales
Question 7
Quelle branche des mathématiques utilise-t-on pour calculer la hauteur ?
L'algèbre linéaire
Les probabilités
La trigonométrie
On se place en effet dans le triangle rectangle $BCH$ et on utilise la relation $\sin(\widehat{C}) = \dfrac{BH}{BC} = \dfrac{\text{hauteur}}{a}$
Question 8
Quelle particularité doit avoir le triangle pour pouvoir appliquer la formule ?
Le triangle doit être équilatéral.
Le triangle doit être quelconque.
En effet, on ne fait aucune hypothèse sur la nature du triangle.
Le triangle doit être isocèle rectangle.
Question 9
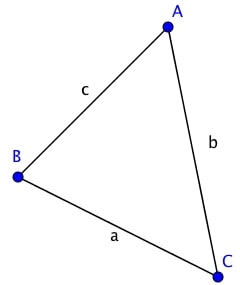
On connait la valeur de $\widehat{A}$ et des trois longueurs des côtés.
Quelle formule utilise-t-on pour calculer l'aire du triangle ?
$\dfrac{1}{2}ab\sin(\widehat{C})$
$\dfrac{1}{2}bc\sin(\widehat{A})$
C'est en effet la bonne formule !
$\dfrac{1}{2}ab\sin(\widehat{A})$
Question 10

On connait la valeur de $\widehat{B}$ et des trois longueurs des côtés.
Quelle formule utilise-t-on pour calculer l'aire du triangle ?
$\dfrac{1}{2}ac\sin(\widehat{C})$
$\dfrac{1}{2}ab\sin(\widehat{B})$
$\dfrac{1}{2}ac\sin(\widehat{B})$
C'est en effet la bonne formule !

C'est en effet la bonne formule.